Kip Thorne and Roger Blandford’s monumental Modern Classical Physics is now available in five stand-alone volumes that make ideal textbooks for individual graduate or advanced undergraduate courses on statistical physics; optics; elasticity and fluid dynamics; plasma physics; and relativity and cosmology. Each volume teaches the fundamental concepts, emphasizes modern, real-world applications, and gives students a physical and intuitive understanding of the subject.
Relativity and Cosmology is an essential introduction to the subject, including remarkable recent advances. Written by award-winning physicists who have made fundamental contributions to the field and taught it for decades, the book differs from most others on the subject in important ways. It highlights recent transformations in our understanding of black holes, gravitational waves, and the cosmos; it emphasizes the physical interpretation of general relativity in terms of measurements made by observers; it explains the physics of the Riemann tensor in terms of tidal forces, differential frame dragging, and associated field lines; it presents an astrophysically oriented description of spinning black holes; it gives a detailed analysis of an incoming gravitational wave’s interaction with a detector such as LIGO; and it provides a comprehensive, in-depth account of the universe’s evolution, from its earliest moments to the present. While the book is designed to be used for a one-quarter or full-semester course, it goes deep enough to provide a foundation for understanding and participating in some areas of cutting-edge research.
- Includes many exercise problems
- Features color figures, suggestions for further reading, extensive cross-references, and a detailed index
- Optional “Track 2” sections make this an ideal book for a one-quarter or one-semester course
- An online illustration package is available to professors
The five volumes, which are available individually as paperbacks and ebooks, are Statistical Physics; Optics; Elasticity and Fluid Dynamics; Plasma Physics; and Relativity and Cosmology.
Awards and Recognition
- Kip S. Thorne, Co-Winner of the 2017 Nobel Prize in Physics
- Roger D. Blandford, Co-Winner of the 2016 Crafoord Prize in Astronomy and Winner of the 2020 Shaw Prize in Astronomy
Kip S. Thorne, winner of the Nobel Prize in physics, is the Feynman Professor Emeritus of Theoretical Physics at Caltech. His books include Gravitation (Princeton) and Black Holes and Time Warps: Einstein’s Outrageous Legacy. Roger D. Blandford, winner of the Crafoord and Shaw prizes in astronomy, is the Luke Blossom Professor in the School of Humanities and Sciences and founding director of the Kavli Institute for Particle Astrophysics and Cosmology at Stanford University.
- List of Boxes
- Preface
- Contents of Modern Classical Physics, volumes 1–5
- PART VII GENERAL RELATIVITY
- 24 From Special to General Relativity
- 24.1 Overview
- 24.2 Special Relativity Once Again
- 24.2.1 Geometric, Frame-Independent Formulation
- 24.2.2 Inertial Frames and Components of Vectors, Tensors, and Physical Laws
- 24.2.3 Light Speed, the Interval, and Spacetime Diagrams
- 24.3 Differential Geometry in General Bases and in Curved Manifolds
- 24.3.1 Nonorthonormal Bases
- 24.3.2 Vectors as Directional Derivatives; Tangent Space; Commutators
- 24.3.3 Differentiation of Vectors and Tensors; Connection Coefficients
- 24.3.4 Integration
- 24.4 The Stress-Energy Tensor Revisited
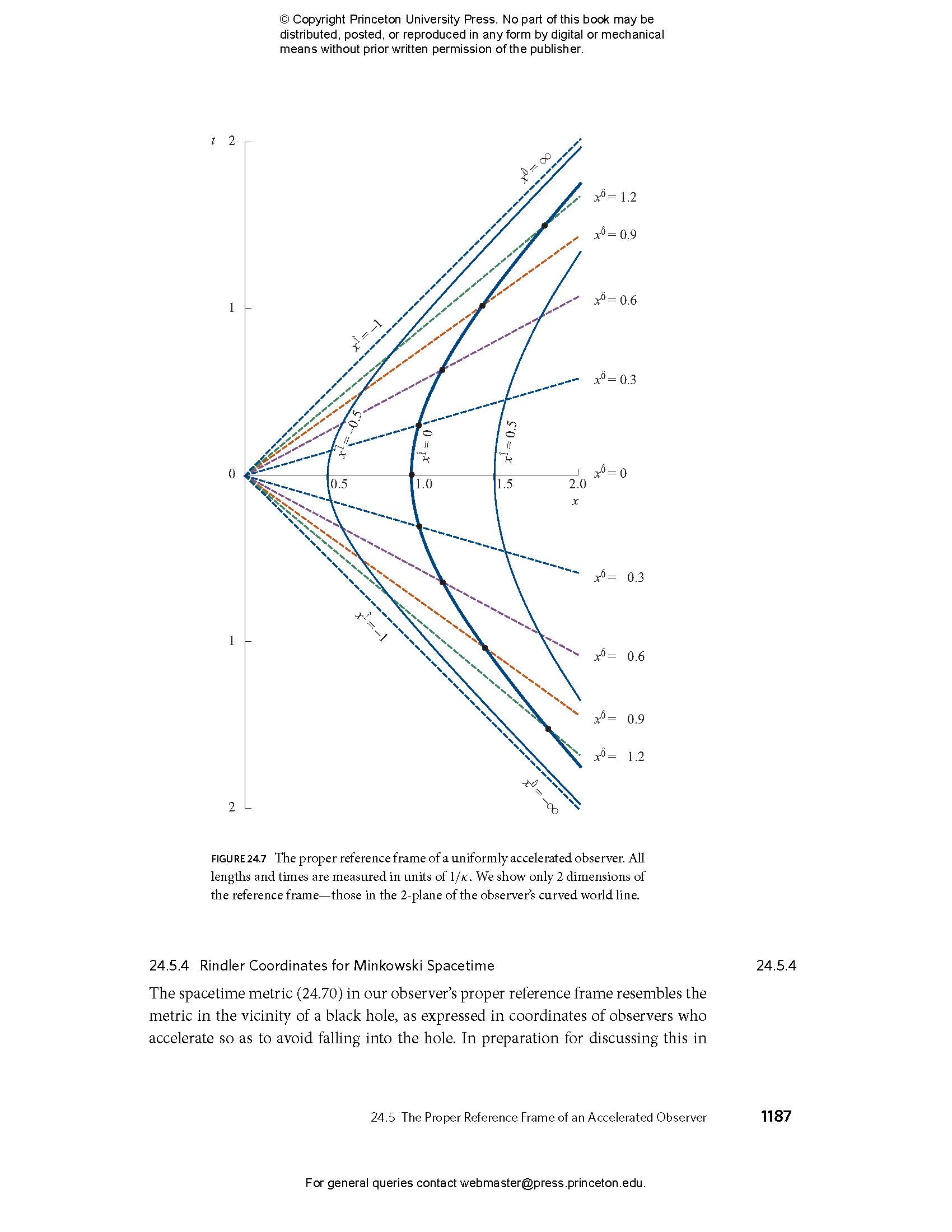
- 24.5 The Proper Reference Frame of an Accelerated Observer
- 24.5.1 Relation to Inertial Coordinates; Metric in Proper Reference Frame; Transport Law for Rotating Vectors
- 24.5.2 Geodesic Equation for a Freely Falling Particle
- 24.5.3 Uniformly Accelerated Observer
- 24.5.4 Rindler Coordinates for Minkowski Spacetime
- Bibliographic Note
- 25 Fundamental Concepts of General Relativity
- 25.1 History and Overview
- 25.2 Local Lorentz Frames, the Principle of Relativity, and Einstein’s Equivalence Principle
- 25.3 The Spacetime Metric, and Gravity as a Curvature of Spacetime
- 25.4 Free-Fall Motion and Geodesics of Spacetime
- 25.5 Relative Acceleration, Tidal Gravity, and Spacetime Curvature
- 25.5.1 Newtonian Description of Tidal Gravity
- 25.5.2 Relativistic Description of Tidal Gravity
- 25.5.3 Comparison of Newtonian and Relativistic Descriptions
- 25.6 Properties of the Riemann Curvature Tensor
- 25.7 Delicacies in the Equivalence Principle, and Some Nongravitational Laws of Physics in Curved Spacetime
- 25.7.1 Curvature Coupling in the Nongravitational Laws
- 25.8 The Einstein Field Equation
- 25.9 Weak Gravitational Fields
- 25.9.1 Newtonian Limit of General Relativity
- 25.9.2 Linearized Theory
- 25.9.3 Gravitational Field outside a Stationary, Linearized Source of Gravity
- 25.9.4 Conservation Laws for Mass, Momentum, and Angular Momentum in Linearized Theory
- 25.9.5 Conservation Laws for a Strong-Gravity Source
- Bibliographic Note
- 26 Relativistic Stars and Black Holes
- 26.1 Overview
- 26.2 Schwarzschild’s Spacetime Geometry
- 26.2.1 The Schwarzschild Metric, Its Connection Coefficients, and Its Curvature Tensors
- 26.2.2 The Nature of Schwarzschild’s Coordinate System, and Symmetries of the Schwarzschild Spacetime
- 26.2.3 Schwarzschild Spacetime at Radii r ≫ M: The Asymptotically Flat Region
- 26.2.4 Schwarzschild Spacetime at r ~ M
- 26.3 Static Stars
- 26.3.1 Birkhoff’s Theorem
- 26.3.2 Stellar Interior
- 26.3.3 Local Conservation of Energy and Momentum
- 26.3.4 The Einstein Field Equation
- 26.3.5 Stellar Models and Their Properties
- 26.3.6 Embedding Diagrams
- 26.4 Gravitational Implosion of a Star to Form a Black Hole
- 26.4.1 The Implosion Analyzed in Schwarzschild Coordinates
- 26.4.2 Tidal Forces at the Gravitational Radius
- 26.4.3 Stellar Implosion in Eddington-Finkelstein Coordinates
- 26.4.4 Tidal Forces at r = 0—The Central Singularity
- 26.4.5 Schwarzschild Black Hole
- 26.5 Spinning Black Holes: The Kerr Spacetime
- 26.5.1 The Kerr Metric for a Spinning Black Hole
- 26.5.2 Dragging of Inertial Frames
- 26.5.3 The Light-Cone Structure, and the Horizon
- 26.5.4 Evolution of Black Holes—Rotational Energy and Its Extraction
- 26.6 The Many-Fingered Nature of Time
- Bibliographic Note
- 27 Gravitational Waves and Experimental Tests of General Relativity
- 27.1 Overview
- 27.2 Experimental Tests of General Relativity
- 27.2.1 Equivalence Principle, Gravitational Redshift, and Global Positioning System
- 27.2.2 Perihelion Advance of Mercury
- 27.2.3 Gravitational Deflection of Light, Fermat’s Principle, and Gravitational Lenses
- 27.2.4 Shapiro Time Delay
- 27.2.5 Geodetic and Lense-Thirring Precession
- 27.2.6 Gravitational Radiation Reaction
- 27.3 Gravitational Waves Propagating through Flat Spacetime
- 27.3.1 Weak, Plane Waves in Linearized Theory
- 27.3.2 Measuring a Gravitational Wave by Its Tidal Forces
- 27.3.3 Gravitons and Their Spin and Rest Mass
- 27.4 Gravitational Waves Propagating through Curved Spacetime
- 27.4.1 Gravitational Wave Equation in Curved Spacetime
- 27.4.2 Geometric-Optics Propagation of Gravitational Waves
- 27.4.3 Energy and Momentum in Gravitational Waves
- 27.5 The Generation of Gravitational Waves
- 27.5.1 Multipole-Moment Expansion
- 27.5.2 Quadrupole-Moment Formalism
- 27.5.3 Quadrupolar Wave Strength, Energy, Angular Momentum, and Radiation Reaction
- 27.5.4 Gravitational Waves from a Binary Star System
- 27.5.5 Gravitational Waves from Binaries Made of Black Holes, Neutron Stars, or Both: Numerical Relativity
- 27.6 The Detection of Gravitational Waves
- 27.6.1 Frequency Bands and Detection Techniques
- 27.6.2 Gravitational-Wave Interferometers: Overview and Elementary Treatment
- 27.6.3 Interferometer Analyzed in TT Gauge
- 27.6.4 Interferometer Analyzed in the Proper Reference Frame of the Beam Splitter
- 27.6.5 Realistic Interferometers
- 27.6.6 Pulsar Timing Arrays
- Bibliographic Note
- 28 Cosmology
- 28.1 Overview
- 28.2 General Relativistic Cosmology
- 28.2.1 Isotropy and Homogeneity
- 28.2.2 Geometry
- 28.2.3 Kinematics
- 28.2.4 Dynamics
- 28.3 The Universe Today
- 28.3.1 Baryons
- 28.3.2 Dark Matter
- 28.3.3 Photons
- 28.3.4 Neutrinos
- 28.3.5 Cosmological Constant
- 28.3.6 Standard Cosmology
- 28.4 Seven Ages of the Universe
- 28.4.1 Particle Age
- 28.4.2 Nuclear Age
- 28.4.3 Photon Age
- 28.4.4 Plasma Age
- 28.4.5 Atomic Age
- 28.4.6 Gravitational Age
- 28.4.7 Cosmological Age
- 28.5 Galaxy Formation
- 28.5.1 Linear Perturbations
- 28.5.2 Individual Constituents
- 28.5.3 Solution of the Perturbation Equations
- 28.5.4 Galaxies
- 28.6 Cosmological Optics
- 28.6.1 Cosmic Microwave Background
- 28.6.2 Weak Gravitational Lensing
- 28.6.3 Sunyaev-Zel’dovich Effect
- 28.7 Three Mysteries
- 28.7.1 Inflation and the Origin of the Universe
- 28.7.2 Dark Matter and the Growth of Structure
- 28.7.3 The Cosmological Constant and the Fate of the Universe
- Bibliographic Note
- App. A Special Relativity: Geometric Viewpoint
- 2.1 Overview
- 2.2 Foundational Concepts
- 2.2.1 Inertial Frames, Inertial Coordinates, Events, Vectors, and Spacetime Diagrams
- 2.2.2 The Principle of Relativity and Constancy of Light Speed
- 2.2.3 The Interval and Its Invariance
- 2.3 Tensor Algebra without a Coordinate System
- 2.4 Particle Kinetics and Lorentz Force without a Reference Frame
- 2.4.1 Relativistic Particle Kinetics:World Lines, 4-Velocity, 4-Momentum and Its Conservation, 4-Force
- 2.4.2 Geometric Derivation of the Lorentz Force Law
- 2.5 Component Representation of Tensor Algebra
- 2.5.1 Lorentz Coordinates
- 2.5.2 Index Gymnastics
- 2.5.3 Slot-Naming Notation
- 2.6 Particle Kinetics in Index Notation and in a Lorentz Frame
- 2.7 Lorentz Transformations
- 2.8 Spacetime Diagrams for Boosts
- 2.9 Time Travel
- 2.9.1 Measurement of Time; Twins Paradox
- 2.9.2 Wormholes
- 2.9.3 Wormhole as Time Machine
- 2.10 Directional Derivatives, Gradients, and the Levi-Civita Tensor
- 2.11 Nature of Electric and Magnetic Fields; Maxwell’s Equations
- 2.12 Volumes, Integration, and Conservation Laws
- 2.12.1 Spacetime Volumes and Integration
- 2.12.2 Conservation of Charge in Spacetime
- 2.12.3 Conservation of Particles, Baryon Number, and Rest Mass
- 2.13 Stress-Energy Tensor and Conservation of 4-Momentum
- 2.13.1 Stress-Energy Tensor
- 2.13.2 4-Momentum Conservation
- 2.13.3 Stress-Energy Tensors for Perfect Fluids and Electromagnetic Fields
- Bibliographic Note
- References
- Name Index
- Subject Index
- Contents of the Unified Work, Modern Classical Physics
- Preface to Modern Classical Physics
- Acknowledgments for Modern Classical Physics
“Extraordinarily impressive.”—Malcolm Longair, Nature
“A magnificent achievement.”—Edward Witten, Physics Today