Years ago, a student in an introductory math class asked me: “Why do you prove everything; why don’t you just tell us?” Ever since, I have pondered that question. One crisp and sensible answer was given by Richard Dedekind in the preface to his 1872 book, translated into English as The Nature and Meaning of Numbers:
In science nothing capable of proof ought to be accepted without proof. An answer that better explains how proof actually works lies in the following anecdote about the 17th-century philosopher Thomas Hobbes, from the delightfully quirky Brief Lives by John Aubrey.
He was 40 yeares old before he looked on Geometry; which happened accidentally. Being in a Gentleman’s Library, Euclid’s Elements lay open, and ’twas the 47 El. Libri 1. He read the proposition. By G—, sayd he (he would now and then sweare an emphaticall Oath by way of emphasis) this is impossible! So he reads the Demonstration of it, which referred him back to such a Proposition; which proposition he read. That referred him back to another, which he also read. Et sic deinceps [and so on] that at last he was demonstratively convinced of that trueth. This made him in love with Geometry.
Thus, a mathematical proof was able to convince Hobbes of something he at first thought was impossible by showing that it follows ultimately from statements—now called axioms—that anybody will accept. This is the axiomatic method, first given in Euclid’s Elements around 300 BCE, and now used by all mathematicians.
At this point, I should admit the Proposition 47 El. Libri 1 that amazed Hobbes was none other than the Pythagorean theorem, well-known to high school students today and in fact well-known before Pythagoras (and Euclid) in several ancient cultures. As most of us recall, the theorem states: the square on the hypotenuse of a right-angled triangle is equal to the sum of the squares on the other two sides. To illustrate: the gray square in the following figure is equal in area to the sum of the areas of the two black squares.

At first sight, this equality is astonishing—it’s no wonder that Hobbes didn’t believe it—but there is a clever way to make it look obvious, probably known since ancient times. Namely, stare at the following two pictures, each containing four copies of the triangle inside a big square.
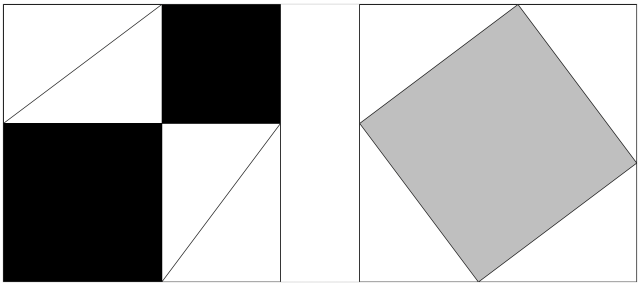
In the first picture, we see that the black squares, which are the squares on two sides of the triangle, equal the big square minus four triangles. In the second picture, we see that the big square minus four triangles equals the gray square, which is the square on the hypotenuse.
Why then did Euclid go to such trouble to prove it? The answer, we believe, lies in a consequence of the Pythagorean theorem, which threw the Pythagorean world into turmoil: the irrationality of the square root of 2.
The square root of 2 arises when the two sides of the triangle are each of length 1, in which case the squares on them are each of area 1. The square on the hypotenuse then has area 1 + 1 = 2 by the Pythagorean theorem and hence the length of the hypotenuse is the square root of 2, √2. But what exactly is √2? The Pythagoreans were shocked to discover that, although they could approximate √2 ever more closely by the fractions 3/2, 7/5, 17/12, 41/29, 99/70, … , no fraction exactly equals √2. This is why we say √2 is irrational, meaning “not a ratio” but also implying that it is unreasonable. It seemed that the world of geometry—the world of lengths, angles, and areas—could not be reconciled with the world of numbers 1, 2, 3, 4, 5, … . The discovery smashed the Pythagorean theory of the world, which held that “all is number.” Legend has it that the discoverer of this unwelcome fact was punished—or suffered divine retribution—by drowning at sea.
At any rate, the apparently irreconcilable differences between numbers and geometry seem to be what led the Greeks to derive geometry from self-evident axioms without the use of numbers. This is really hard to do. For example, one has to rethink what the “sum” of squares means, and what it means for this “sum” to “equal” another square. It is also necessary to express everything in language so clear that no misunderstanding is possible. But the axiomatic method set up by Euclid to overcome these difficulties has endured to the present day. It is true that there are some small gaps in Euclid’s Elements, which have since been fixed, but the axiomatic method remains unrivalled and is the model for the way mathematics is done today. There are also now more comprehensive axiom systems, which succeed in unifying the worlds of both geometry and numbers.
While the axiomatic method is flawless in principle, the way proofs are actually written is open to human error. Like anyone else, mathematicians can make mistakes, and in very long proofs—which became common in the 20th century—mistakes can be hard to find. They tend to hide in places where the author skips some tedious or repetitive details, often with remarks like “it is easy to check that” or “the proof is similar to the previous case.” However, it is possible to avoid mistakes the same way one avoids mistakes in calculation: by mechanizing the process. This can be done because a complete proof must be understandable to every competent reader, which amounts to being checkable without thinking—and hence checkable by machine. So mechanizing the process of proof is basically the same as mechanizing calculation.
Unfortunately, writing machine-checkable proofs requires enormous human labor as well as intimate knowledge of the relevant mathematics. To date, only a handful of really long proofs have been rewritten in machine-checkable form. (And the original human-generated proofs have indeed been found essentially correct.) Among the proofs that await rewriting in machine-checkable form—or even in a form understandable to expert mathematicians—the most notorious example concerns the so-called abc-conjecture. This conjecture is a somewhat technical one concerning the prime factors of numbers a, b, c in the simple equation a + b = c, but it is of interest to number theorists because it has many remarkable consequences.
Since 2012, a small group of mathematicians has distributed what they believe to be a proof of the abc-conjecture. This “proof” has failed to convince most experts in number theory, who point to what seems to be a gap in the “proof.” Thus, there has been a 10-year dispute between the two groups, whom I will call (to avoid mentioning names) the abc-believers and the abc-skeptics. In principle, their dispute could be resolved by converting the “proof” to machine-checkable form. But the abc-believers claim this is unnecessary and that the only problem is “ignorance” on the part of the abc-skeptics.
This strange affair became even stranger in recent months, when the abc-believers turned toward the history of mathematics. Likening themselves to the hapless, persecuted Pythagorean who discovered the irrationality √2, they warned of “dire consequences” if the abc-skeptics prevail.
Well, we shall see. But history tells us that if the abc-believers want to emulate Euclid and rebuild mathematics to accommodate their ideas, they must first write in a language that everyone can understand.
Let’s hope it will not come this (cartoon by Sidney Harris):

John Stillwell is emeritus professor of mathematics at the University of San Francisco. His many books include Elements of Mathematics and Reverse Mathematics (both Princeton).

