As the size and complexity of data continue to grow exponentially across the physical sciences, machine learning is helping scientists to sift through and analyze this information while driving breathtaking advances in quantum physics, astronomy, cosmology, and beyond. This incisive textbook covers the basics of building, diagnosing, optimizing, and deploying machine learning methods to solve research problems in physics and astronomy, with an emphasis on critical thinking and the scientific method. Using a hands-on approach to learning, Machine Learning for Physics and Astronomy draws on real-world, publicly available data as well as examples taken directly from the frontiers of research, from identifying galaxy morphology from images to identifying the signature of standard model particles in simulations at the Large Hadron Collider.
- Introduces readers to best practices in data-driven problem-solving, from preliminary data exploration and cleaning to selecting the best method for a given task
- Each chapter is accompanied by Jupyter Notebook worksheets in Python that enable students to explore key concepts
- Includes a wealth of review questions and quizzes
- Ideal for advanced undergraduate and early graduate students in STEM disciplines such as physics, computer science, engineering, and applied mathematics
- Accessible to self-learners with a basic knowledge of linear algebra and calculus
- Slides and assessment questions (available only to instructors)
Awards and Recognition
- Winner of the Chambliss Astronomical Writing Award, American Astronomical Society
Viviana Acquaviva is professor of physics at the New York City College of Technology and the Graduate Center, City University of New York, and the recipient of a PIVOT fellowship to apply AI tools to problems in climate. She was named one of Italy’s fifty most inspiring women in technology by InspiringFifty, which recognizes women in STEM who serve as role models for girls around the world.
- Preface
- 1 Introduction to Machine Learning Methods
- 1.1 What Is Machine Learning?
- 1.2 What Can We Do with It?
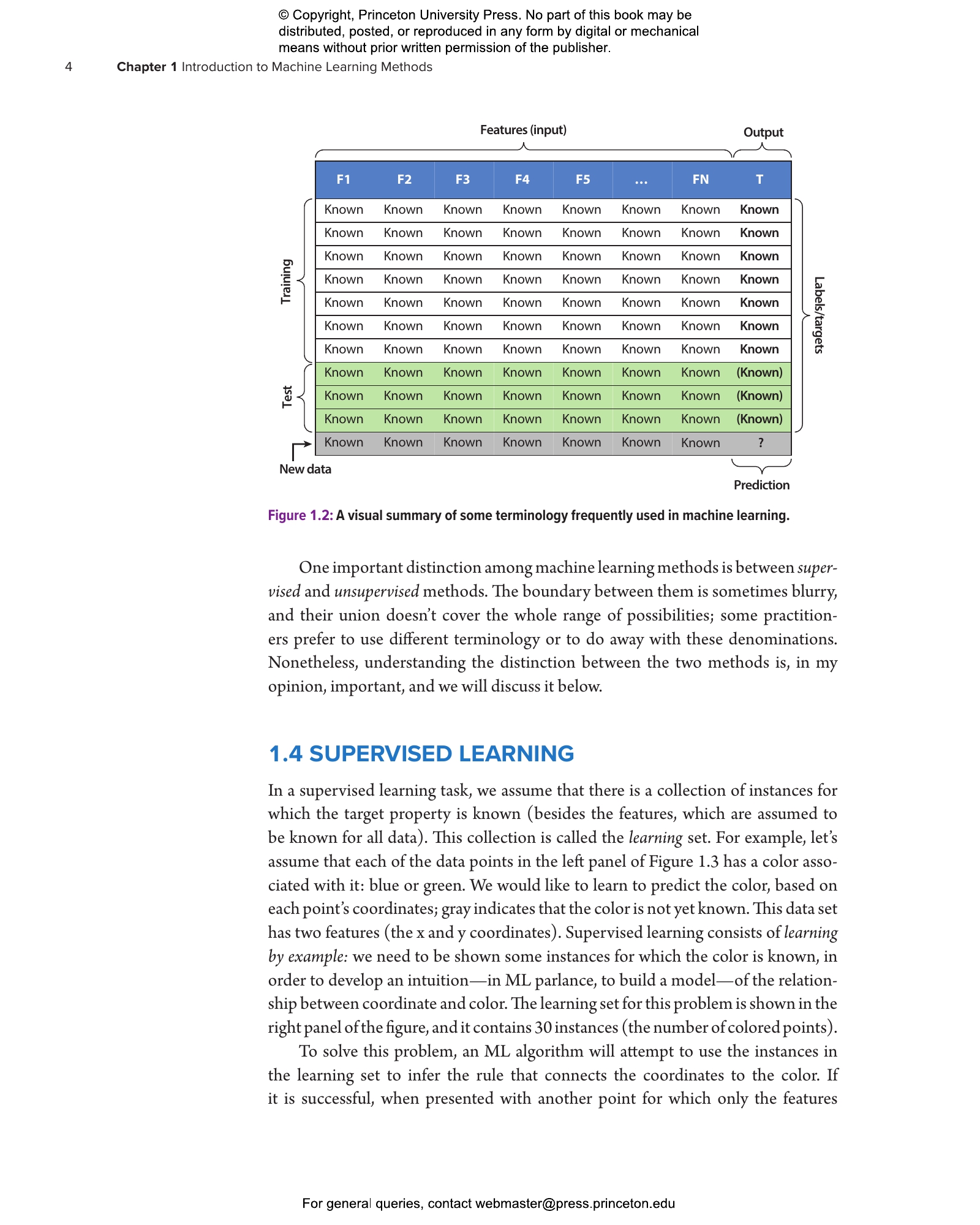
- 1.3 The Language of Machine Learning
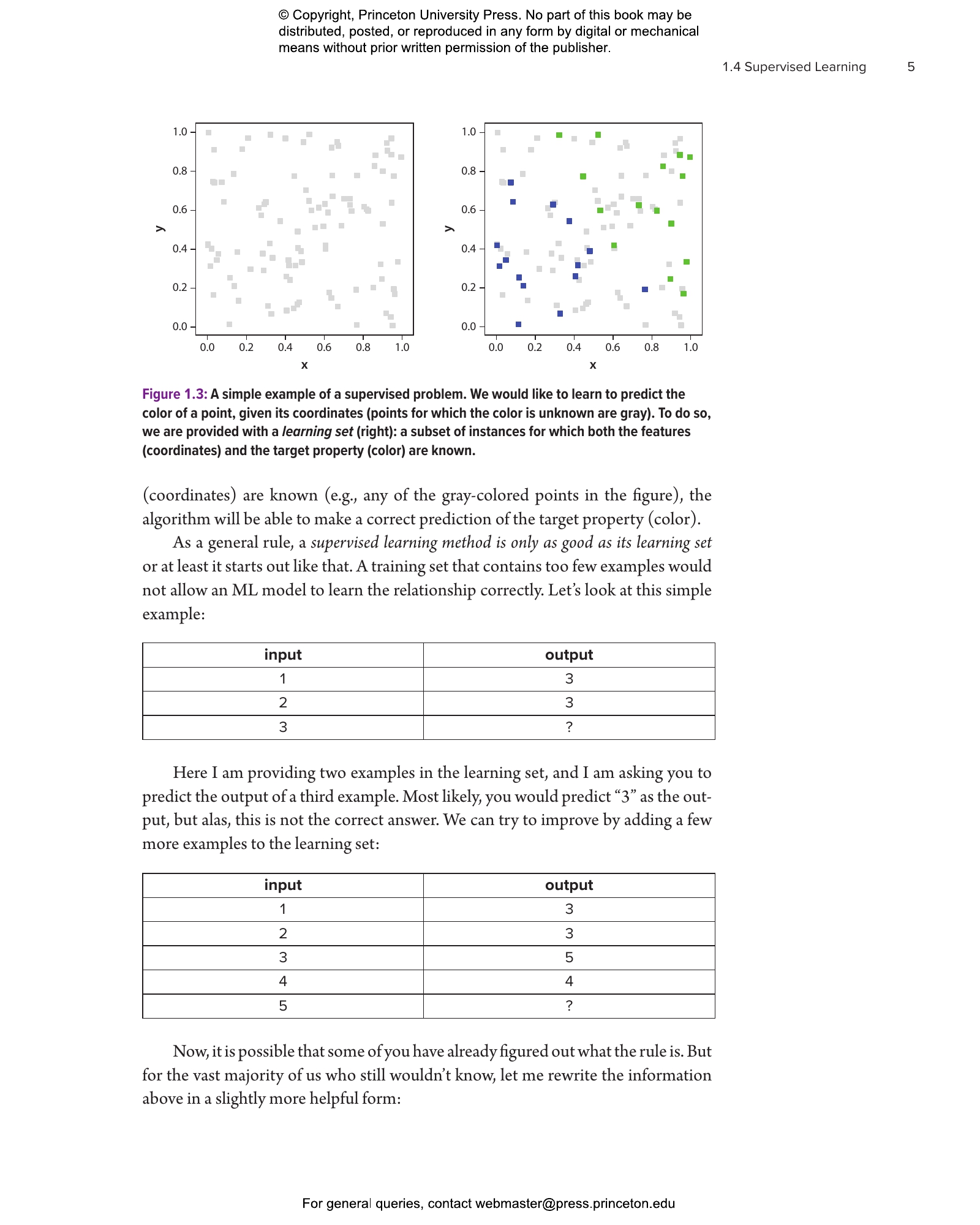
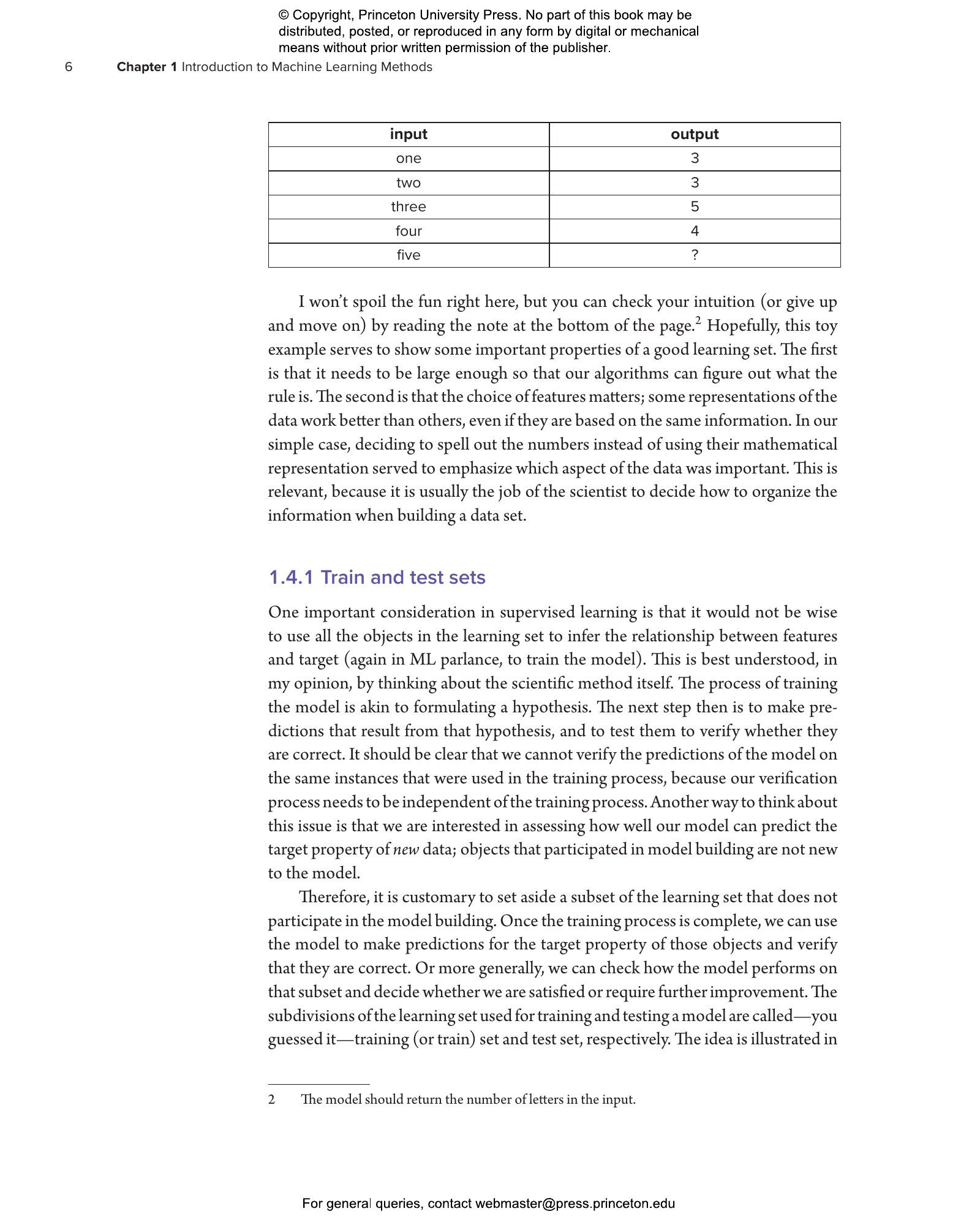
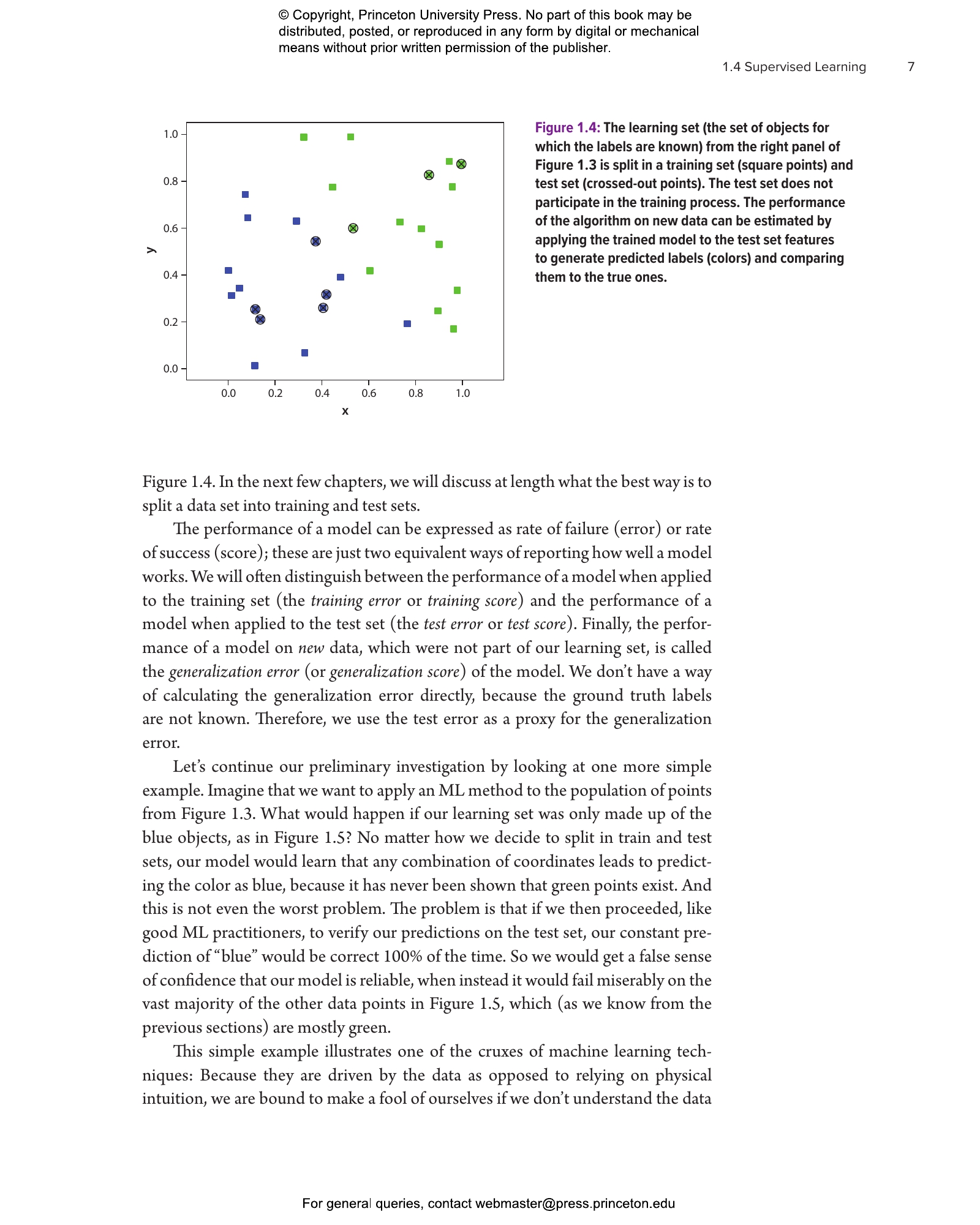
- 1.4 Supervised Learning
- 1.5 Unsupervised Learning
- 1.6 Machine Learning versus Inference
- 1.7 Review and Discussion Questions
- 1.8 Programming Exercises
- 2 First Supervised Models: Neighbors and Trees
- 2.1 Building an ML Model
- 2.2 Decision Trees
- 2.3 kNN: Finding Neighbors
- 2.4 Lessons Learned
- 2.5 Review and Discussion Questions
- 2.6 Programming Exercises
- 3 Supervised Classification: Evaluation and Diagnostics
- 3.1 Working with Research-level Data Sets: Preprocessing and Analysis
- 3.2 Binary Classification Evaluation
- 3.3 Choosing an Evaluation Metric
- 3.4 Beyond Training and Testing: Cross Validation
- 3.5 Diagnosing a Supervised Classification Model
- 3.6 Improving a Supervised Classification Model
- 3.7 Beyond Binary Classification
- 3.8 Lessons Learned
- 3.9 Review and Discussion Questions
- 3.10 Programming Exercises
- 4 Supervised Learning Models: Optimization
- 4.1 Data Set Description
- 4.2 A New Algorithm: Support Vector Machines
- 4.3 Data Exploration and Preprocessing
- 4.4 Diagnosis
- 4.5 Hyperparameter Optimization
- 4.6 Feature Engineering
- 4.7 Further Diagnostics and Final Model Selection
- 4.8 Lessons Learned
- 4.9 Review and Discussion Questions
- 4.10 Programming Exercises
- 5 Regression
- 5.1 From Classification to Regression: What’s New in the Analysis Pipeline?
- 5.2 Linear Regression
- 5.3 Linear Models and Loss Functions
- 5.4 Gradient Descent
- 5.5 Bias-variance Trade-off
- 5.6 Regularization
- 5.7 Generalized Linear Models
- 5.8 Poisson Regression
- 5.9 Lessons Learned
- 5.10 Review and Discussion Questions
- 5.11 Programming Exercises
- 6 Ensemble Methods
- 6.1 Bias-variance Decomposition for Ensembles
- 6.2 A Three-dimensional Map of the Universe
- 6.3 Bagging Methods
- 6.4 Bagging Algorithms for Photometric Redshifts
- 6.5 Boosting Methods
- 6.6 Boosting Methods for Photometric Redshifts
- 6.7 Feature Importance
- 6.8 Lessons Learned
- 6.9 Review and Discussion Questions
- 6.10 Programming Exercises
- 7 Clustering and Dimensionality Reduction
- 7.1 Clustering
- 7.2 Density-based Clustering
- 7.3 Mixture Models
- 7.4 Dimensionality Reduction
- 7.5 Application: Hyperspectral Images Analysis
- 7.6 So Close, No Matter How Far: The Importance of Distance Metrics
- 7.7 Other Nonlinear Mapping Techniques
- 7.8 Supervised or Unsupervised Dimensionality Reduction?
- 7.9 Lessons Learned
- 7.10 Review and Discussion Questions
- 7.11 Programming Exercises
- 8 Introduction to Neural Networks
- 8.1 Deep Learning and Why It Works
- 8.2 Assembling a Neural Network
- 8.3 Have Network, Will Train
- 8.4 Two Worked Examples: Particle Classification and Photometric Redshifts
- 8.5 Beyond Fully Connected Networks
- 8.6 Lessons Learned
- 8.7 Review and Discussion Questions
- 8.8 Programming Exercises
- 9 Summary and Additional Resources
- 9.1 Have Problem, Have Data: What Next?
- 9.2 Additional Resources
- 9.3 Conclusion
- References
- Index
“A self-contained introduction for students with a physics or astronomy background. Acquaviva is clearly an experienced practitioner of machine learning for physics and gives many useful tips.”—David Rousseau, coeditor of Artificial Intelligence for High Energy Physics
“Machine Learning for Physics and Astronomy covers the essential concepts of machine learning algorithms in detail, with accessible examples and practical applications.”—Claudia Scarlata, University of Minnesota
“A wonderful introduction to the field. Acquaviva uses an engaging, conversational tone that breaks through the algorithmic details and welcomes the reader into the marvelously expansive world of machine learning.”—John Bochanski, Rider University
“This book features a very high level of scholarship with an outstanding breadth of material that manages to be instructive and complete while not overwhelming students. With clear language and plenty of examples, it has just the right depth and coverage for higher-level college classes that incorporate machine learning in a physics and astronomy setting.”—Benne Holwerda, University of Louisville