This lab guide accompanies the textbook Quantitative Biosciences, providing students with the skills they need to translate biological principles and mathematical concepts into computational models of living systems. This hands-on guide uses a case study approach organized around central questions in the life sciences, introducing landmark advances in the field while teaching students—whether from the life sciences, physics, computational sciences, engineering, or mathematics—how to reason quantitatively in the face of uncertainty.
- Draws on real-world case studies in molecular and cellular biosciences, organismal behavior and physiology, and populations and ecological communities
- Encourages good coding practices, clear and understandable modeling, and accessible presentation of results
- Helps students to develop a diverse repertoire of simulation approaches, enabling them to model at the appropriate scale
- Builds practical expertise in a range of methods, including sampling from probability distributions, stochastic branching processes, continuous time modeling, Markov chains, bifurcation analysis, partial differential equations, and agent-based simulations
- Bridges the gap between the classroom and research discovery, helping students to think independently, troubleshoot and resolve problems, and embark on research of their own
- Stand-alone computational lab guides for Quantitative Biosciences also available in Python and MATLAB
Joshua S. Weitz is professor and the Clark Leadership Chair in Data Analytics in the Department of Biology at the University of Maryland. Previously, he held the Tom and Marie Patton Chair in Biological Sciences at the Georgia Institute of Technology, where he founded the Interdisciplinary Graduate Program in Quantitative Biosciences. He is the author of Quantitative Viral Ecology (Princeton). Marian Domínguez-Mirazo is a PhD candidate in Quantitative Biosciences in the School of Biological Sciences at the Georgia Institute of Technology.
- Preface
- The goal
- You can do it
- Acknowledgments
- Part I Molecular and Cellular Biosciences
1 Fluctuations and the Nature of Mutations- 1.1 Hands-on approach to mutations and selection
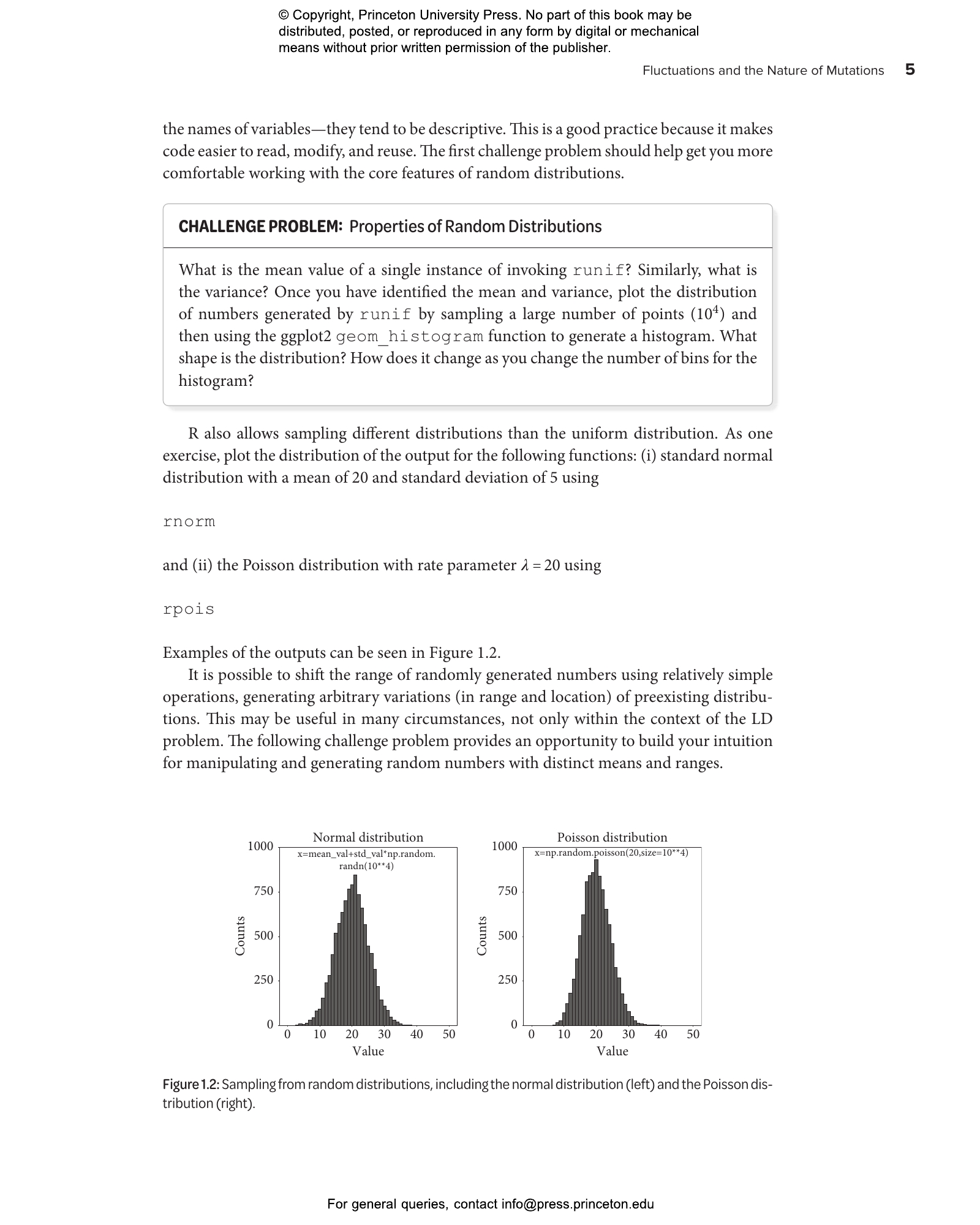
- 1.2 Sampling from provided distributions
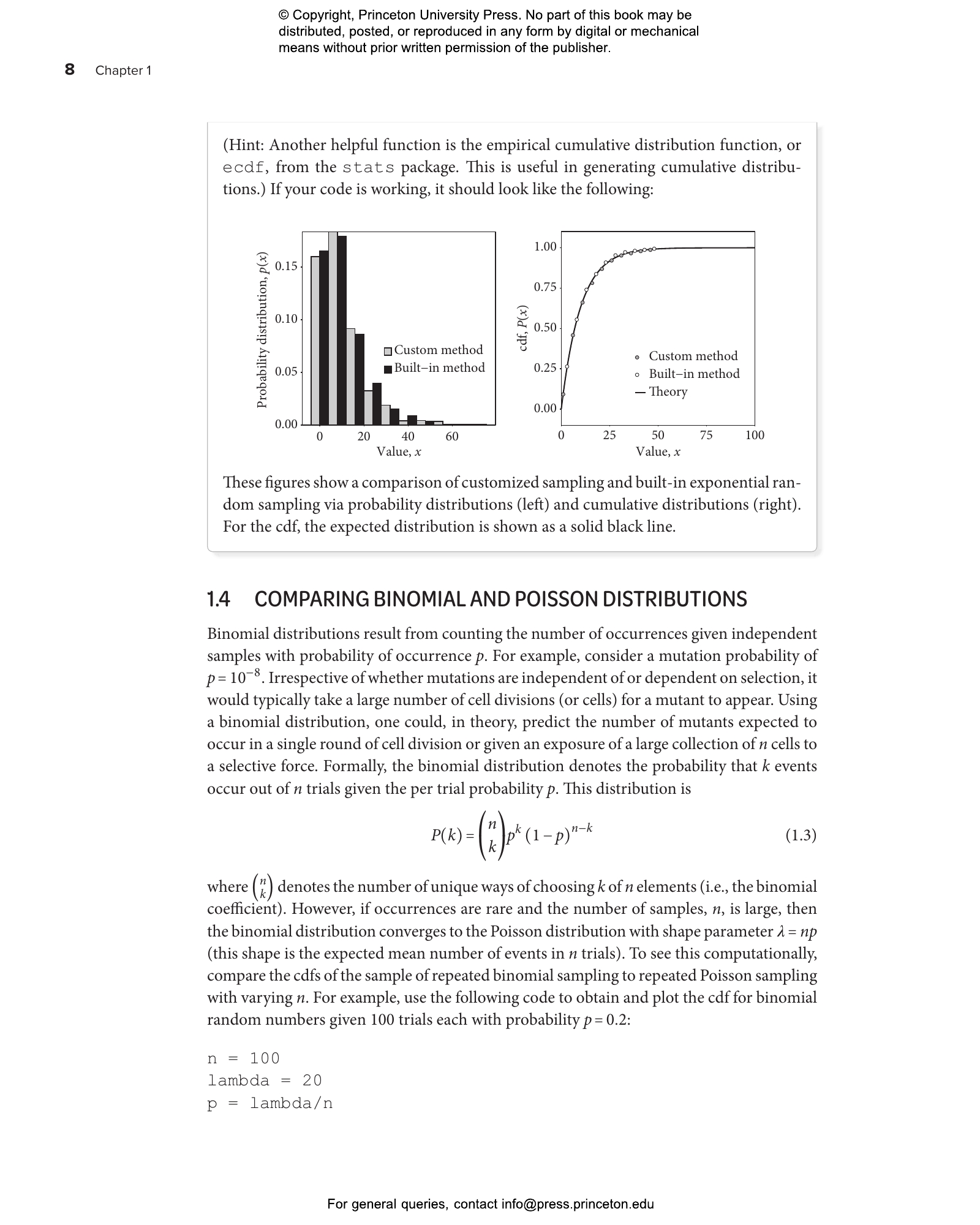
- 1.3 Sampling from custom distributions
- 1.4 Comparing binomial and Poisson distributions
- 1.5 The start of dynamics
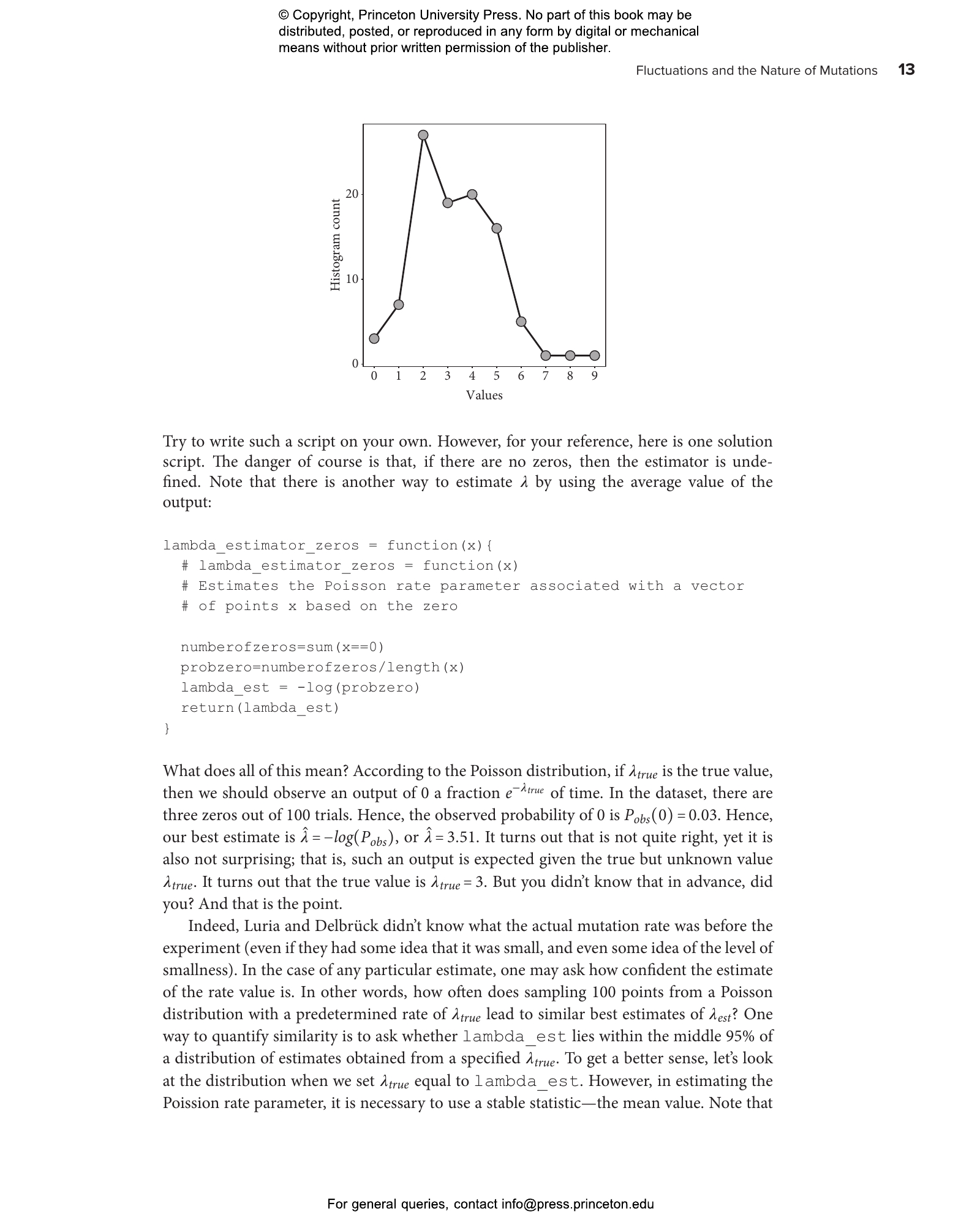
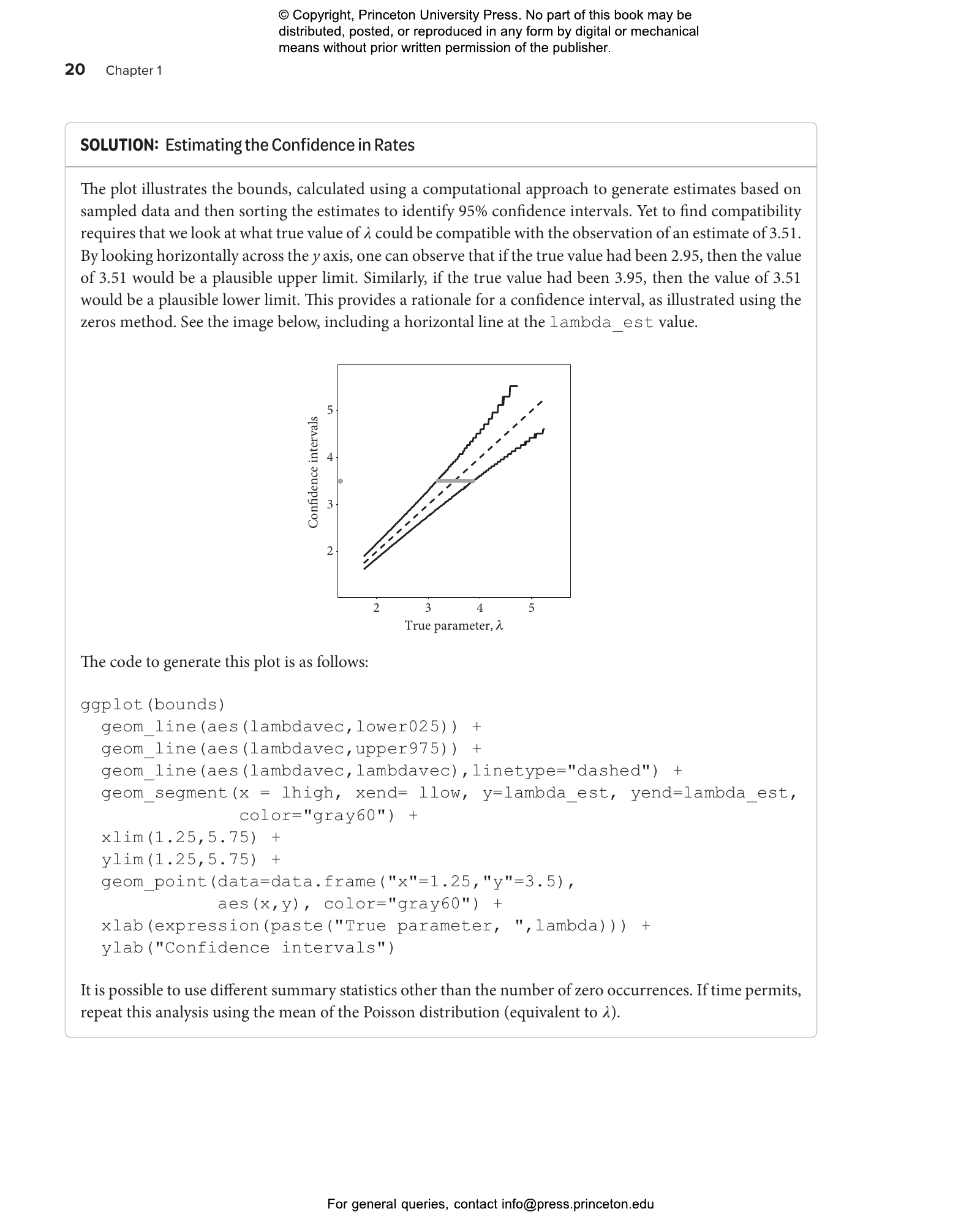
- 1.6 Inferring parameters from data
2 Bistability of Genetic Circuits- 2.1 Continuous models of cellular dynamics and gene regulation
- 2.2 Simulating coupled ordinary differential equations
- 2.3 Qualitative analysis of nonlinear dynamical systems
- 2.4 Evaluating the local stability of equilibria
- 2.5 Bistability and bifurcation diagrams
3 Stochastic Gene Expression and Cellular Variability- 3.1 Simulating stochastic gene expression
- 3.2 Poisson processes: Finding the time of the next event
- 3.3 A theory of timing given multiple stochastic processes
- 3.4 Gillespie algorithm applied to a gene expression model
- 3.5 Loading and saving data
4 Evolutionary Dynamics: Mutations, Selection, and Diversity- 4.1 Modeling evolutionary dynamics
- 4.2 Transition matrices in Markov processes
- 4.3 The Wright-Fisher model
- Part II Organismal Behavior and Physiology
5 Robust Sensing and Chemotaxis- 5.1 Toward chemotaxis in single-celled organisms
- 5.2 Enzyme kinetics
- 5.3 Time-dependent functions in differential equations
- 5.4 Probability distribution redux
- 5.5 E. coli movement
6 Nonlinear Dynamics and Signal Processing in Neurons- 6.1 Computational neuroscience
- 6.2 The Hodgkin-Huxley model
- 6.3 Firing without a current
- 6.4 Neuron dynamics: Thresholds in magnitude and time
- 6.5 Technical appendix
7 Excitations and Signaling, from Cells to Tissue- 7.1 Excitable media: From localized to spatial dynamics
- 7.2 FitzHugh-Nagumo: The ODE model
- 7.3 FitzHugh-Nagumo: One-dimensional PDEs
8 Organismal Locomotion through Water, Air, and Earth- 8.1 Introduction
- 8.2 The internal origins of movement
- 8.3 Orbits in configuration space
- 8.4 From Borelli to Newton and back again
- 8.5 The greatest gait of all
- Part III Populations and Ecological Communities
9 Flocking and Collective Behavior: When Many Become One- 9.1 Agent-based models and emergence in flocks
- 9.2 The Vicsek model
- 9.3 Flocking dynamics
- 9.4 Bonus: SPP and the power of leadership
10 Conflict and Cooperation Among Individuals and Populations- 10.1 Strategies, games, and populations
- 10.2 Mean field replicator dynamics of microbial games
- 10.3 Stochastic versions of microbial games
- 10.4 Type VI secretion—a killer game, in space
11 Eco-evolutionary Dynamics- 11.1 From predation events to population dynamics
- 11.2 Ecological dynamics when evolution is fast
- 11.3 Functional responses—a microscopic approach
12 Outbreak Dynamics: From Prediction to Control- 12.1 Outbreaks: From deterministic models to stochastic realizations
- 12.2 Epidemic model—fundamentals
- 12.3 Stochastic epidemics
- Part IV The Future of Ecosystems
13 Ecosystems: Chaos, Tipping Points, and Catastrophes- 13.1 Modeling complexity: An enabling view
- 13.2 Small differences, big effects
- 13.3 Explosive growth and population catastrophes
- 13.4 Small models of a big climate
- 13.5 Coda