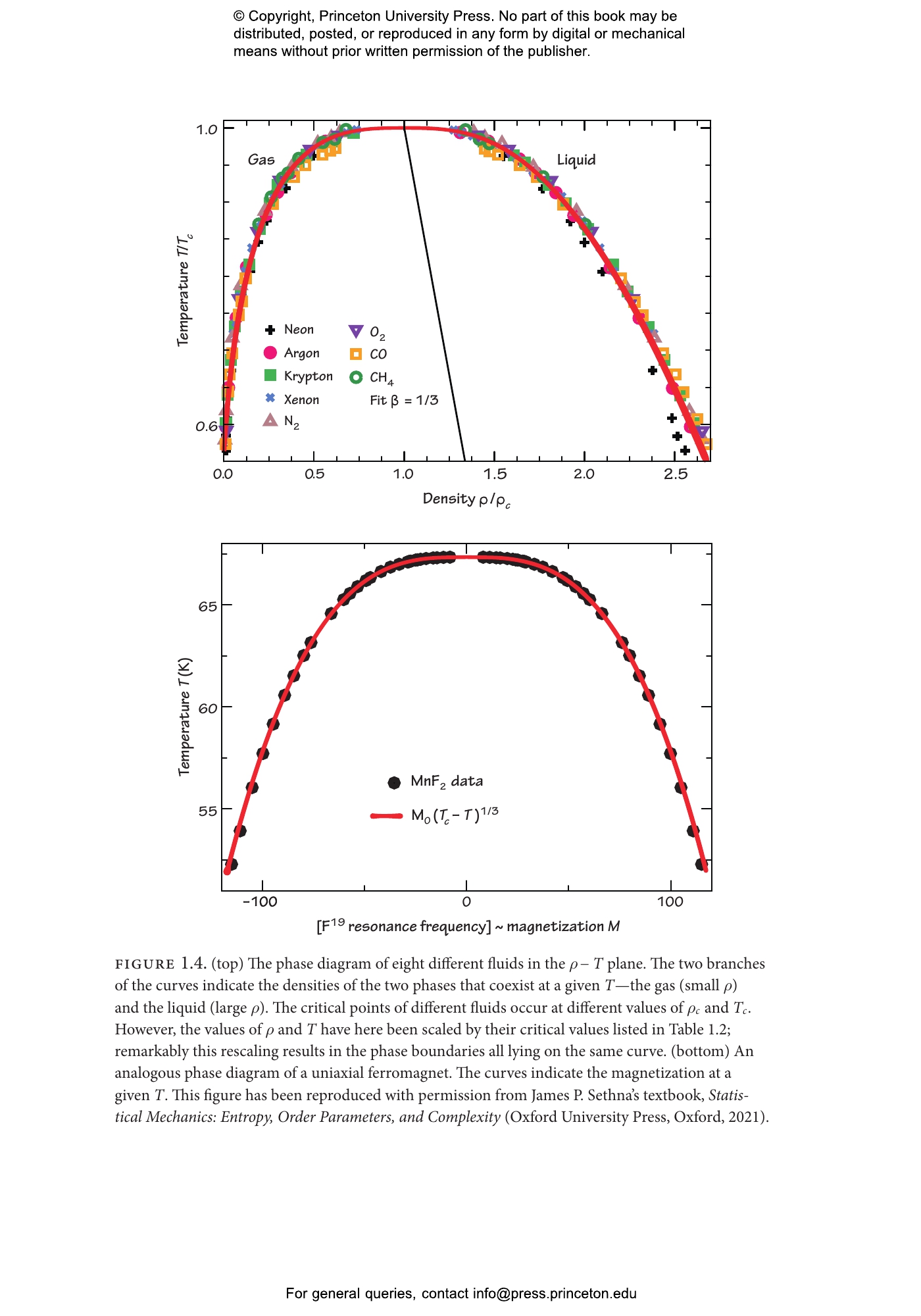
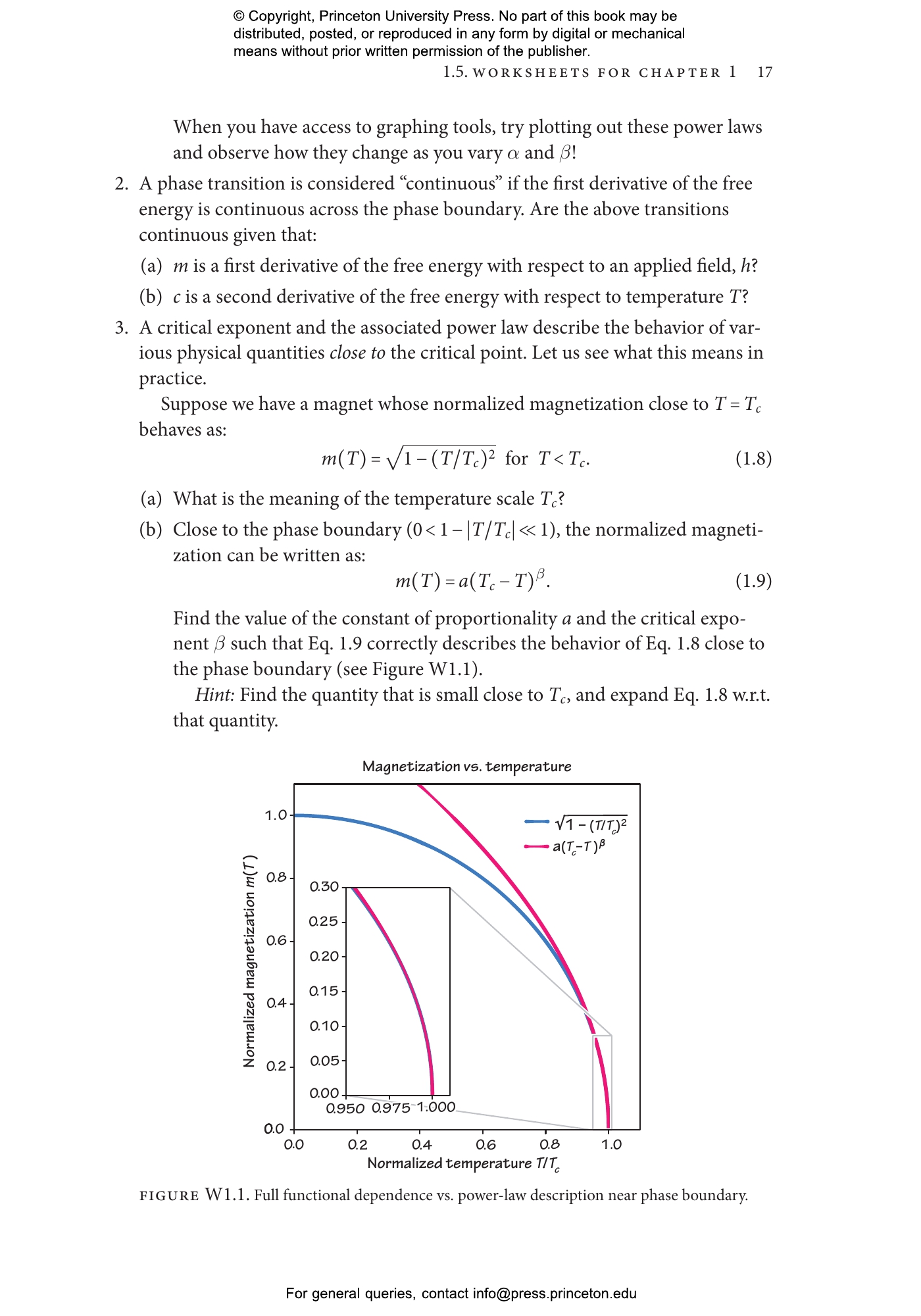
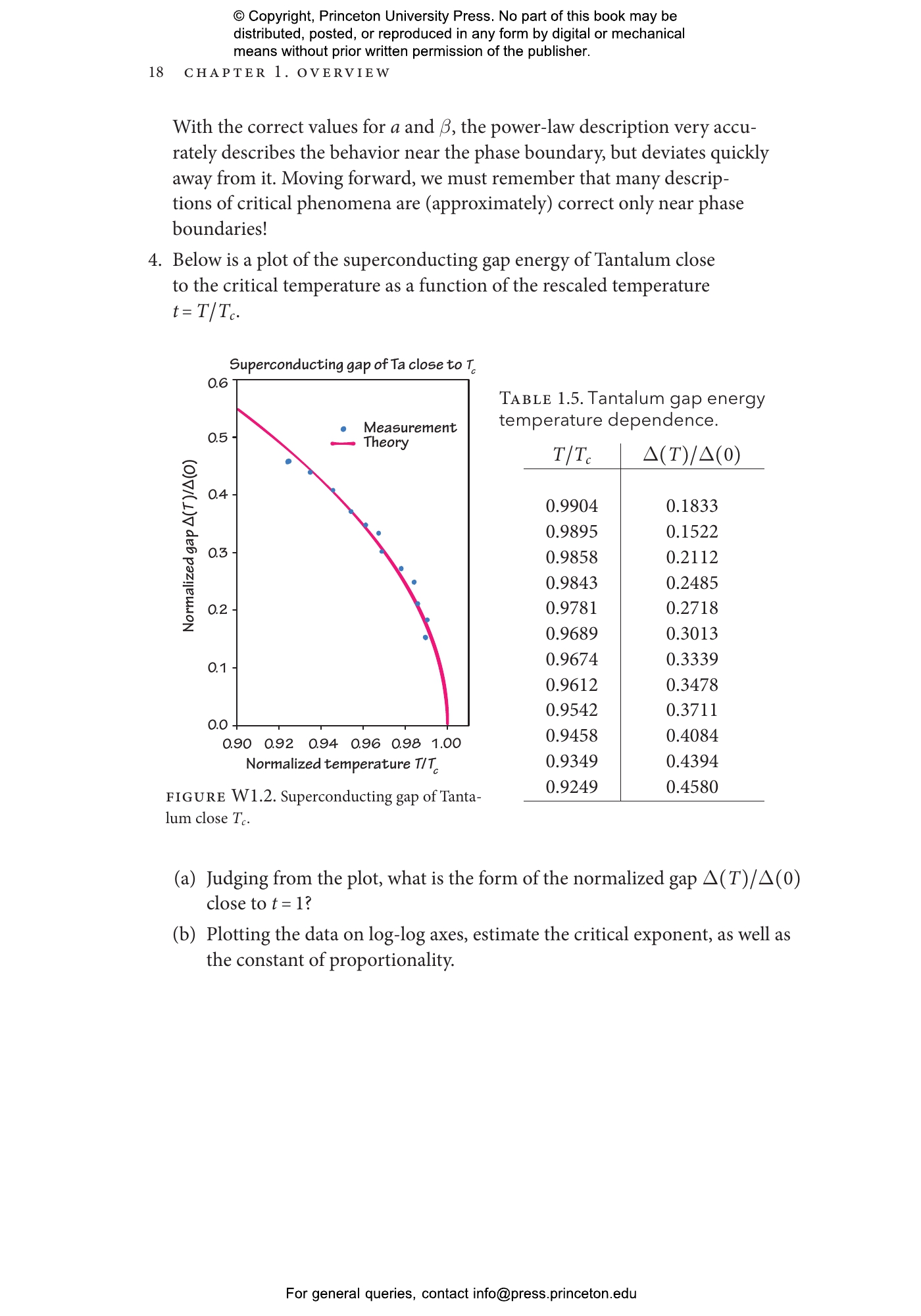
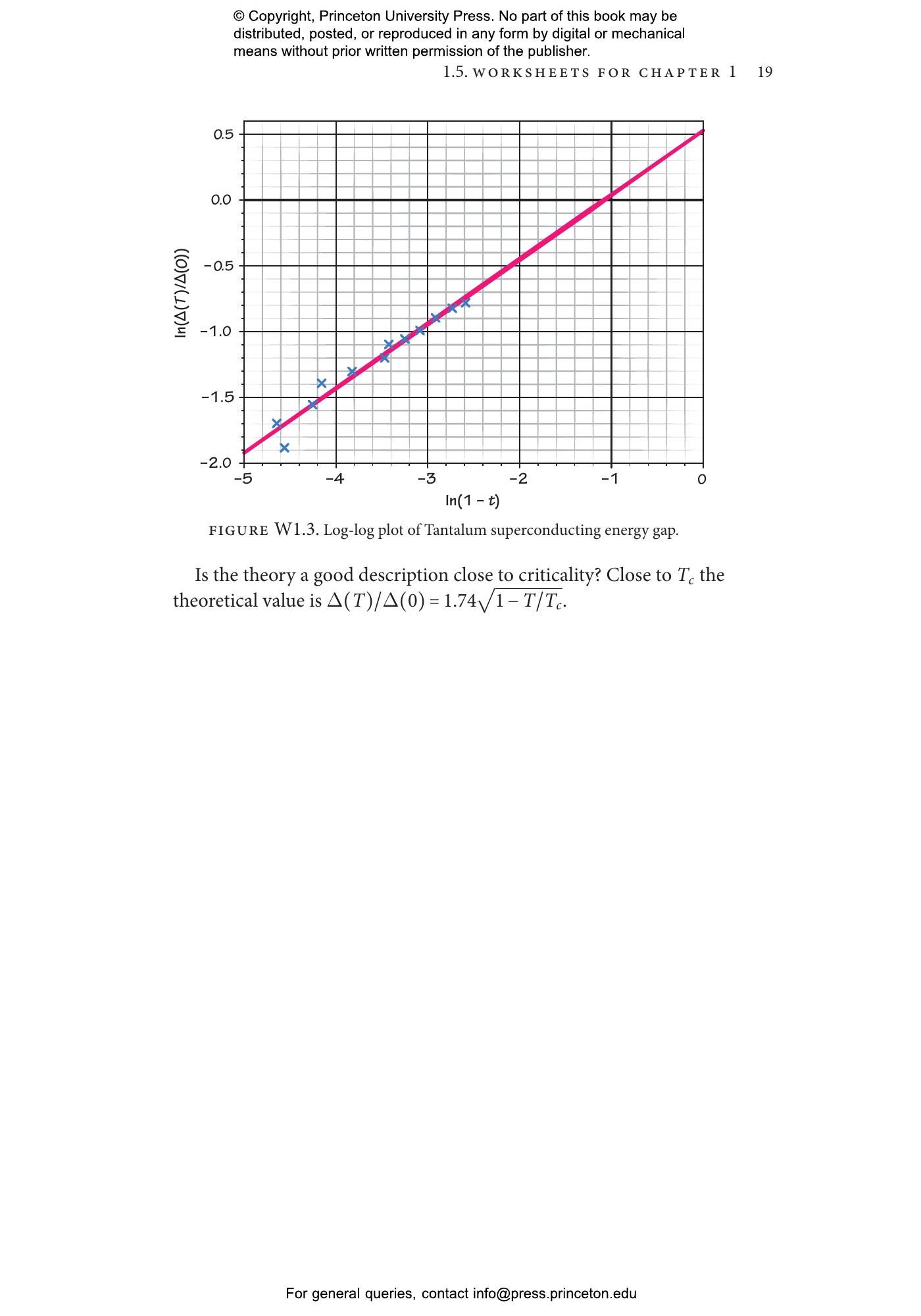
Statistical Mechanics of Phases and Phase Transitions


Hardcover
Paperback
ebook
- Sale Price:
- $52.50/£43.40
- Price:
-
$75.00/£62.00 - ISBN:
- Published:
- Apr 9, 2024
- Copyright:
- 2024
- 49 color illus.
- Main_subject:
- Physics & Astronomy
30% off with code PUP30
Statistical mechanics deploys a powerful set of mathematical approaches for studying the thermodynamic properties of complex physical systems. This textbook introduces students to the statistical mechanics of systems undergoing changes of state, focusing on the basic principles for classifying distinct thermodynamic phases and the critical phenomena associated with transitions between them. Uniquely designed to promote active learning, Statistical Mechanics of Phases and Phase Transitions presents some of the most beautiful and profound concepts in physics, enabling students to obtain an essential understanding of a computationally challenging subject without getting lost in the details.
- Provides a self-contained, conceptually deep introduction to the statistical mechanics of phases and phase transitions from a modern perspective
- Carefully leads students from spontaneously broken symmetries to the universality of phase transitions and the renormalization group
- Encourages student-centric active learning suitable for both the classroom and self-study
- Features a wealth of guided worksheets with full solutions throughout the book that help students learn by doing
- Includes informative appendixes that cover key mathematical concepts and methods
- Ideal for undergraduate physics majors and beginning graduate students
- Solutions manual for all end-of-chapter problems (available only to instructors)