What Can Be Computed? is a uniquely accessible yet rigorous introduction to the most profound ideas at the heart of computer science. Crafted specifically for undergraduates who are studying the subject for the first time, and requiring minimal prerequisites, the book focuses on the essential fundamentals of computer science theory and features a practical approach that uses real computer programs (Python and Java) and encourages active experimentation. It is also ideal for self-study and reference.
The book covers the standard topics in the theory of computation, including Turing machines and finite automata, universal computation, nondeterminism, Turing and Karp reductions, undecidability, time-complexity classes such as P and NP, and NP-completeness, including the Cook-Levin Theorem. But the book also provides a broader view of computer science and its historical development, with discussions of Turing’s original 1936 computing machines, the connections between undecidability and Gödel’s incompleteness theorem, and Karp’s famous set of twenty-one NP-complete problems.
Throughout, the book recasts traditional computer science concepts by considering how computer programs are used to solve real problems. Standard theorems are stated and proven with full mathematical rigor, but motivation and understanding are enhanced by considering concrete implementations. The book’s examples and other content allow readers to view demonstrations of—and to experiment with—a wide selection of the topics it covers. The result is an ideal text for an introduction to the theory of computation.
- An accessible and rigorous introduction to the essential fundamentals of computer science theory, written specifically for undergraduates taking introduction to the theory of computation
- Features a practical, interactive approach using real computer programs (Python in the text, with forthcoming Java alternatives online) to enhance motivation and understanding
- Gives equal emphasis to computability and complexity
- Includes special topics that demonstrate the profound nature of key ideas in the theory of computation
- Lecture slides and Python programs are available at whatcanbecomputed.com
John MacCormick is associate professor of computer science at Dickinson College and a leading teacher, researcher, and writer in his field. He has a PhD in computer vision from the University of Oxford and has worked in the research labs of Hewlett-Packard and Microsoft. His previous books include Nine Algorithms That Changed the Future: The Ingenious Ideas That Drive Today's Computers (Princeton). Erik Demaine and Martin Demaine created the curved crease sculpture featured on the cover of What Can Be Computed? Cover photo courtesy of the artists.
- Acknowledgments
- Preface for instructors
- The inspiration of GEB
- Which “theory” course are we talking about?
- The features that might make this book appealing
- What’s in and what’s out
- Possible courses based on this book
- Computer science as a liberal art
- OVERVIEW
- 1 INTRODUCTION: WHAT CAN AND CANNOT BE COMPUTED?
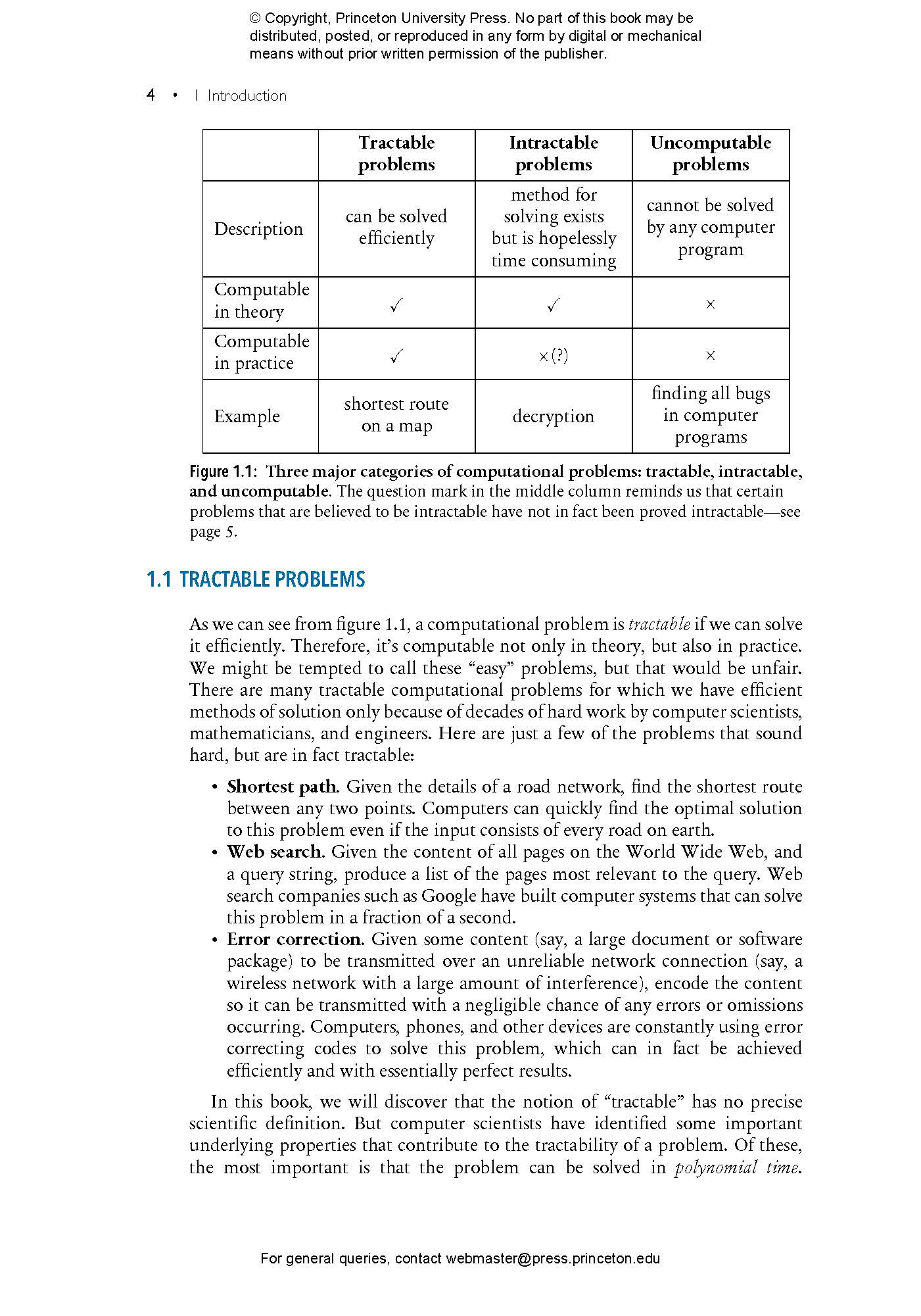
- 1.1 Tractable problems
- 1.2 Intractable problems
- 1.3 Uncomputable problems
- 1.4 A more detailed overview of the book
- Overview of part I: Computability theory
- Overview of part II: Complexity theory
- Overview of part III: Origins and applications
- 1.5 Prerequisites for understanding this book
- 1.6 The goals of the book
- The fundamental goal: What can be computed?
- Secondary goal 1: A practical approach
- Secondary goal 2: Some historical insight
- 1.7 Why study the theory of computation?
- Reason 1: The theory of computation is useful
- Reason 2: The theory of computation is beautiful and important
- Exercises
- Part I: COMPUTABILITY THEORY
- 2 WHAT IS A COMPUTER PROGRAM?
- 2.1 Some Python program basics
- Editing and rerunning a Python program
- Running a Python program on input from a file
- Running more complex experiments on Python programs
- 2.2 SISO Python programs
- Programs that call other functions and programs
- 2.3 ASCII characters and multiline strings
- 2.4 Some problematic programs
- 2.5 Formal definition of Python program
- 2.6 Decision programs and equivalent programs
- 2.7 Real-world programs versus SISO Python programs
- 3 SOME IMPOSSIBLE PYTHON PROGRAMS
- 3.1 Proof by contradiction
- 3.2 Programs that analyze other programs
- Programs that analyze themselves
- 3.3 The program yesOnString.py
- 3.4 The program yesOnSelf.py
- 3.5 The program notYesOnSelf.py
- 3.6 yesOnString.py can’t exist either
- A compact proof that yesOnString.py can’t exist
- 3.7 Perfect bug-finding programs are impossible
- 3.8 We can still find bugs, but we can’t do it perfectly
- 4 WHAT IS A COMPUTATIONAL PROBLEM?
- 4.1 Graphs, alphabets, strings, and languages
- Graphs
- Trees and rooted trees
- Alphabets
- Strings
- Languages
- 4.2 Defining computational problems
- Positive and negative instances
- Notation for computational problems
- 4.3 Categories of computational problems
- Search problems
- Optimization problems
- Threshold problems
- Function problems
- Decision problems
- Converting between general and decision problems
- Complement of a decision problem
- Computational problems with two input strings
- 4.4 The formal definition of “solving” a problem
- 4.5 Recognizing and deciding languages
- Recognizable languages
- Recursive and recursively enumerable languages
- Exercises
- 5 TURING MACHINES: THE SIMPLEST COMPUTERS
- 5.1 Definition of a Turing machine
- Halting and looping
- Accepters and transducers
- Abbreviated notation for state diagrams
- Creating your own Turing machines
- 5.2 Some nontrivial Turing machines
- The moreCsThanGs machine
- The countCs machine
- Important lessons from the countCs example
- 5.3 From single-tape Turing machines to multi-tape Turing machines
- Two-tape, single-head Turing machines
- Two-way infinite tapes
- Multi-tape, single-head Turing machines
- Two-tape, two-head Turing machines
- 5.4 From multi-tape Turing machines to Python programs and beyond
- Multi-tape Turing machine → random-access Turing machine
- Random-access Turing machine → real computer
- Modern computer → Python program
- 5.5 Going back the other way: Simulating a Turing machine with Python
- A serious caveat: Memory limitations and other technicalities
- 5.6 Classical computers can simulate quantum computers
- 5.7 All known computers are Turing equivalent
- 6 UNIVERSAL COMPUTER PROGRAMS: PROGRAMS THAT CAN DO ANYTHING
- 6.1 Universal Python programs
- 6.2 Universal Turing machines
- 6.3 Universal computation in the real world
- 6.4 Programs that alter other programs
- Ignoring the input and performing a fixed calculation instead
- 6.5 Problems that are undecidable but recognizable
- 7 REDUCTIONS: HOW TO PROVE A PROBLEM IS HARD
- 7.1 A reduction for easiness
- 7.2 A reduction for hardness
- 7.3 Formal definition of Turing reduction
- Why “Turing” reduction?
- Oracle programs
- Why is ≤T used to denote a Turing reduction?
- Beware the true meaning of “reduction”
- 7.4 Properties of Turing reductions
- 7.5 An abundance of uncomputable problems
- The variants of YESONSTRING
- The halting problem and its variants
- Uncomputable problems that aren’t decision problems
- 7.6 Even more uncomputable problems
- The computational problem COMPUTESF
- Rice’s theorem
- 7.7 Uncomputable problems that aren’t about programs
- 7.8 Not every question about programs is uncomputable
- 7.9 Proof techniques for uncomputability
- Technique 1: The reduction recipe
- Technique 2: Reduction with explicit Python programs
- Technique 3: Apply Rice’s theorem
- Exercises
- 8 NONDETERMINISM: MAGIC OR REALITY?
- 8.1 Nondeterministic Python programs
- 8.2 Nondeterministic programs for nondecision problems
- 8.3 Computation trees
- 8.4 Nondeterminism doesn’t change what is computable
- 8.5 Nondeterministic Turing machines
- 8.6 Formal definition of nondeterministic Turing machines
- 8.7 Models of nondeterminism
- 8.8 Unrecognizable problems
- 8.9 Why study nondeterminism?
- 9 FINITE AUTOMATA: COMPUTING WITH LIMITED RESOURCES
- 9.1 Deterministic finite automata
- 9.2 Nondeterministic finite automata
- State diagrams for nfas
- Formal definition of an nfa
- How does an nfa accept a string?
- Sometimes nfas make things easier
- 9.3 Equivalence of nfas and dfas
- Nondeterminism can affect computability: The example of pdas
- Practicality of converted nfas
- Minimizing the size of dfas
- 9.4 Regular expressions
- Pure regular expressions
- Standard regular expressions
- Converting between regexes and finite automata
- 9.5 Some languages aren’t regular
- The nonregular language GnTn
- The key difference between Turing machines and finite automata
- 9.6 Many more nonregular languages
- 9.7 Combining regular languages
- Part II: COMPUTATIONAL COMPLEXITY THEORY
- 10 COMPLEXITY THEORY: WHEN EFFICIENCY DOES MATTER
- 10.1 Complexity theory uses asymptotic running times
- 10.2 Big-O notation
- Dominant terms of functions
- A practical definition of big-O notation
- Superpolynomial and subexponential
- Other asymptotic notation
- Composition of polynomials is polynomial
- Counting things with big-O
- 10.3 The running time of a program
- Running time of a Turing machine
- Running time of a Python program
- The lack of rigor in Python running times
- 10.4 Fundamentals of determining time complexity
- A crucial distinction: The length of the input versus the numerical value of the input
- The complexity of arithmetic operations
- Beware of constant-time arithmetic operations
- The complexity of factoring
- The importance of the hardness of factoring
- The complexity of sorting
- 10.5 For complexity, the computational model does matter
- Simulation costs for common computational models
- Multi-tape simulation has quadratic cost
- Random-access simulation has cubic cost
- Universal simulation has logarithmic cost
- Real computers cost only a constant factor
- Python programs cost the same as real computers
- Python programs can simulate random-access Turing machines efficiently
- Quantum simulation may have exponential cost
- All classical computational models differ by only polynomial factors
- Our standard computational model: Python programs
- 10.6 Complexity classes
- 11 Poly AND Expo: THE TWO MOST FUNDAMENTAL COMPLEXITY CLASSES
- 11.1 Definitions of Poly and Expo
- Poly and Expo compared to P, Exp, and FP
- 11.2 Poly is a subset of Expo
- 11.3 A first look at the boundary between Poly and Expo
- ALL3SETS and ALLSUBSETS
- Traveling salespeople and shortest paths
- Multiplying and factoring
- Back to the boundary between Poly and Expo
- Primality testing is in Poly
- 11.4 Poly and Expo don’t care about the computational model
- 11.5 HALTEx: A decision problem in Expo but not Poly
- 11.6 Other problems that are outside Poly
- 11.7 Unreasonable encodings of the input affect complexity
- 11.8 Why study Poly, really?
- 12 PolyCheck AND NPoly: HARD PROBLEMS THAT ARE EASY TO VERIFY
- 12.1 Verifiers
- 12.2 Polytime verifiers
- Bounding the length of proposed solutions and hints
- Verifying negative instances in exponential time
- Solving arbitrary instances in exponential time
- 12.3 The complexity class PolyCheck
- Some PolyCheck examples: PACKING,SUBSETSUM, and PARTITION
- The haystack analogy for PolyCheck
- 12.4 The complexity class NPoly
- 12.5 PolyCheck and NPoly are identical
- Every PolyCheck problem is in NPoly
- Every NPoly problem is in PolyCheck
- 12.6 The PolyCheck/NPoly sandwich
- 12.7 Nondeterminism does seem to change what is computable efficiently
- 12.8 The fine print about NPoly
- An alternative definition of NPoly
- NPoly compared to NP and FNP
- Exercises
- 13 POLYNOMIAL-TIME MAPPING REDUCTIONS: PROVING X IS AS EASY AS Y
- 13.1 Definition of polytime mapping reductions
- Polyreducing to nondecision problems
- 13.2 The meaning of polynomial-time mapping reductions
- 13.3 Proof techniques for polyreductions
- 13.4 Examples of polyreductions using Hamilton cycles
- A polyreduction from UHC to DHC
- A polyreduction from DHC to UHC
- 13.5 Three satisfiability problems: CIRCUITSAT, SAT, and 3-SAT
- Why do we study satisfiability problems?
- CIRCUITSAT
- SAT
- Conjunctive normal form
- ASCII representation of Boolean formulas
- 3-SAT
- 13.6 Polyreductions between CIRCUITSAT, SAT, and 3-SAT
- The Tseytin transformation
- 13.7 Polyequivalence and its consequences
- 14 NP-COMPLETENESS: MOST HARD PROBLEMS ARE EQUALLY HARD
- 14.1 P versus NP
- 14.2 NP-completeness
- Reformulations of P versus NP using NP-completeness
- 14.3 NP-hardness
- 14.4 Consequences of P=NP
- 14.5 CIRCUITSAT is a “hardest” NP problem
- 14.6 NP-completeness is widespread
- 14.7 Proof techniques for NP-completeness
- 14.8 The good news and bad news about NP-completeness
- Problems in NPoly but probably not NP-hard
- Some problems that are in P
- Some NP-hard problems can be approximated efficiently
- Some NP-hard problems can be solved efficiently for real-world inputs
- Some NP-hard problems can be solved in pseudo-polynomial time
- Exercises
Part III: ORIGINS AND APPLICATIONS- 15 THE ORIGINAL TURING MACHINE
- 15.1 Turing’s definition of a “computing machine”
- 15.2 Machines can compute what humans can compute
- 15.3 The Church–Turing thesis: A law of nature?
- The equivalence of digital computers
- Church’s thesis: The equivalence of computer programs and algorithms
- Turing’s thesis: The equivalence of computer programs and human brains
- Church–Turing thesis: The equivalence of all computational processes
- Exercises
- 16 YOU CAN’T PROVE EVERYTHING THAT’S TRUE
- The history of computer proofs
- 16.1 Mechanical proofs
- Semantics and truth
- Consistency and completeness
- Decidability of logical systems
- 16.2 Arithmetic as a logical system
- Converting the halting problem to a statement about integers
- Recognizing provable statements about integers
- The consistency of Peano arithmetic
- 16.3 The undecidability of mathematics
- 16.4 The incompleteness of mathematics
- 16.5 What have we learned and why did we learn it?
- 17 KARP’S 21 PROBLEMS
- 17.1 Karp’s overview
- 17.2 Karp’s definition of NP-completeness
- 17.3 The list of 21 NP-complete problems
- 17.4 Reductions between the 21 NP-complete problems
- Polyreducing SAT to CLIQUE
- Polyreducing CLIQUE to NODE COVER
- Polyreducing DHC to UHC
- Polyreducing SAT to 3-SAT
- Polyreducing KNAPSACK to PARTITION
- 17.5 The rest of the paper: NP-hardness and more
- 18 CONCLUSION: WHAT WILL BE COMPUTED?
- 18.1 The big ideas about what can be computed
BibliographyIndex
"The concept is excellent, and it fills an important gap in the available textbooks on computation theory."—Kitty Meeks, London Mathematical Society
"This wonderful book explores the theory of computing from a practical viewpoint. John MacCormick covers the basic concepts of computability and complexity, what we can and cannot compute—keeping the material grounded by connecting it with Python—the popular programming language."—Lance Fortnow, author of The Golden Ticket: P, NP, and the Search for the Impossible
"This well-designed, well-written, and accessible book assumes minimal prerequisites, explains the intuition behind its proofs, and has the unique feature of using Python as a computational model, which makes the presentation practical. I especially like its inclusion of historical content."—Jianfeng Lu, Duke University
"I would love to adopt this text for my introduction to theory of computation course. The level and coverage is perfect for undergraduates. The text hits the sweet spot by carefully presenting the ideas without an overwhelming level of mathematical sophistication. I want my students to come away from the course with the big ideas rather than struggling through mathematical notation and formal proofs, and this text does exactly that. I love that the main computational model is Python, and I think this makes the content more real for students."—Jill Zimmerman, Goucher College
"What Can Be Computed? should succeed brilliantly in capturing the imagination of students. Using Python as a model of computation, MacCormick is able to introduce the greatest ideas in computer science theory as quickly and intuitively as possible. On the other hand, no rigor is ever lost. Over and over, he finds ways to take very complex concepts and boil them down to small and concrete components. Core concepts are presented in a beautiful and accessible way."—Matt Franklin, University of California, Davis