The Probability Lifesaver: All the Tools You Need to Understand Chance
The essential lifesaver for students who want to master probability
-
Series:
- Princeton Lifesaver Study Guides
Hardcover
- Price:
- $29.95/£25.00
- ISBN:
- Published:
- May 16, 2017
- Copyright:
- 2017
- Pages:
- 752
- Size:
- 7 x 10 in.
- Illus:
- 8 color illus. 64 line illus. 21 tables.
Paperback
- Price:
- $29.95/£25.00
- ISBN:
- Published:
- May 16, 2017
- Copyright:
- 2017
- Pages:
- 752
- Size:
- 7 x 10 in.
- Illus:
- 8 color illus. 64 line illus. 21 tables.
ebook
- Price:
- $29.95/£25.00
- ISBN:
- Published:
- May 16, 2017
- Copyright:
- 2017
- Pages:
- 752
- Size:
- 7 x 10 in.
- Illus:
- 8 color illus. 64 line illus. 21 tables.
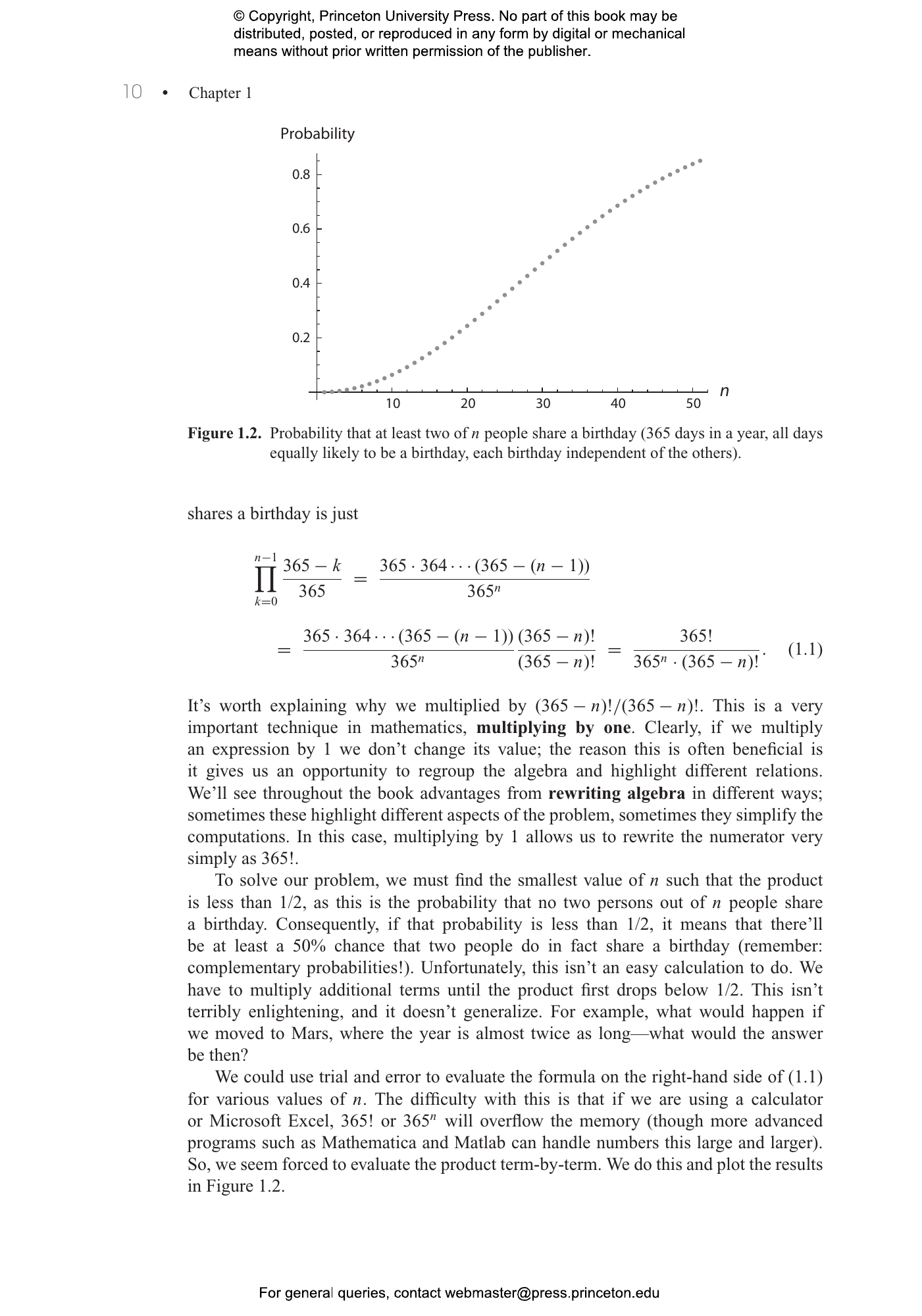
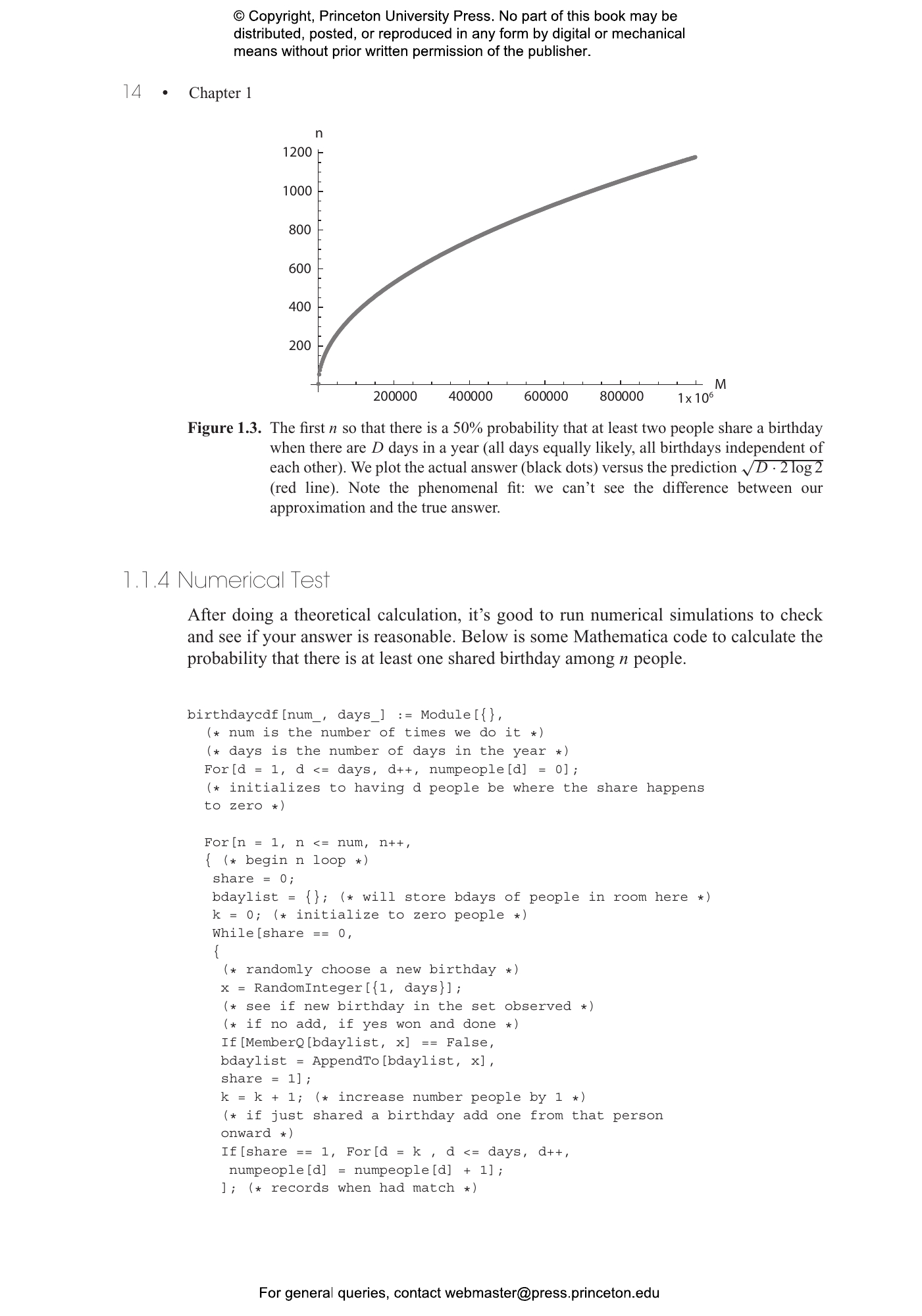
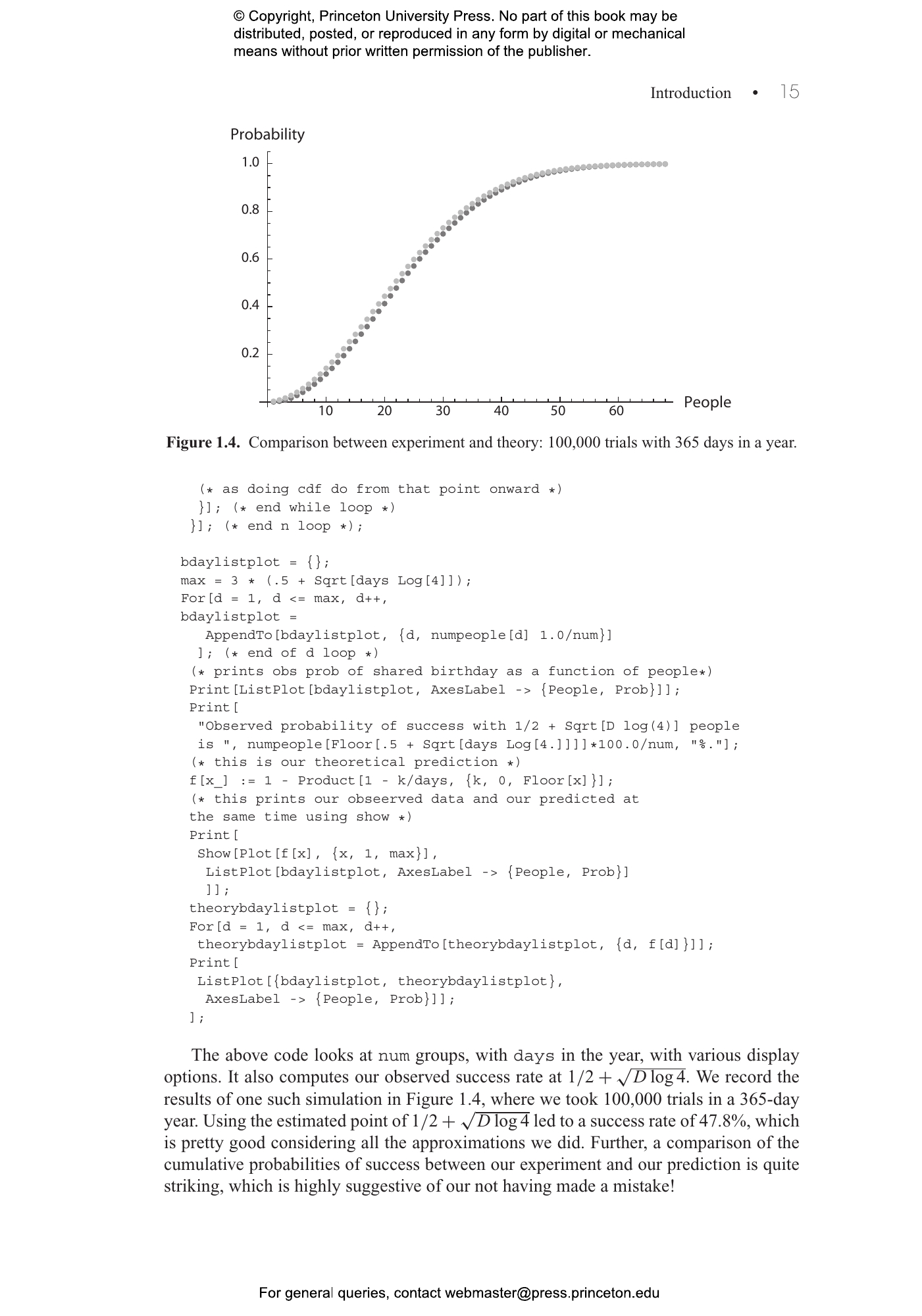
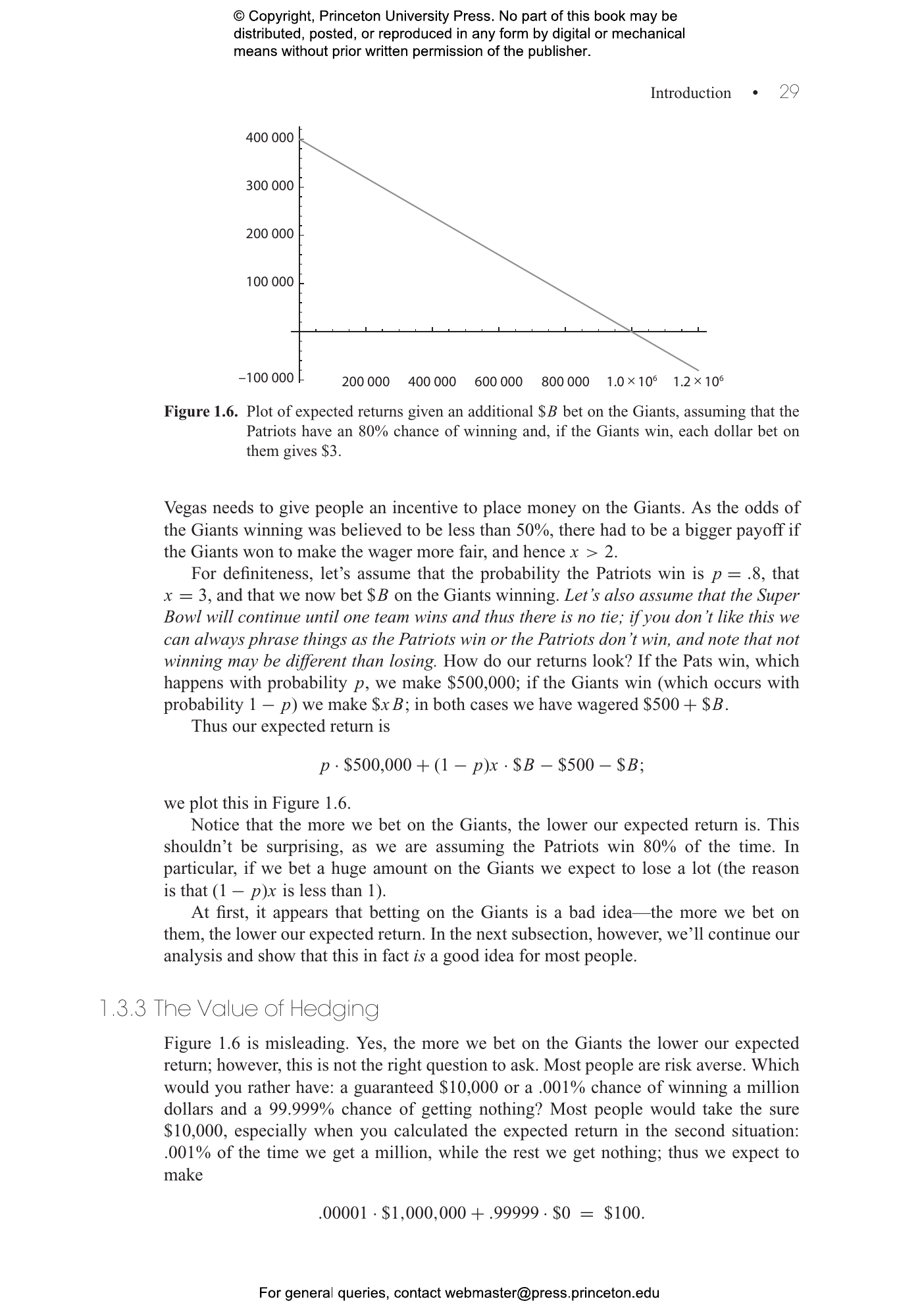
For students learning probability, its numerous applications, techniques, and methods can seem intimidating and overwhelming. That’s where The Probability Lifesaver steps in. Designed to serve as a complete stand-alone introduction to the subject or as a supplement for a course, this accessible and user-friendly study guide helps students comfortably navigate probability’s terrain and achieve positive results.
The Probability Lifesaver is based on a successful course that Steven Miller has taught at Brown University, Mount Holyoke College, and Williams College. With a relaxed and informal style, Miller presents the math with thorough reviews of prerequisite materials, worked-out problems of varying difficulty, and proofs. He explores a topic first to build intuition, and only after that does he dive into technical details. Coverage of topics is comprehensive, and materials are repeated for reinforcement—both in the guide and on the book’s website. An appendix goes over proof techniques, and video lectures of the course are available online. Students using this book should have some familiarity with algebra and precalculus.
The Probability Lifesaver not only enables students to survive probability but also to achieve mastery of the subject for use in future courses.
- A helpful introduction to probability or a perfect supplement for a course
- Numerous worked-out examples
- Lectures based on the chapters are available free online
- Intuition of problems emphasized first, then technical proofs given
- Appendixes review proof techniques
- Relaxed, conversational approach
- Note to Readers
- How to Use This Book
- I General Theory
- 1 Introduction
- 1.1 Birthday Problem
- 1.1.1 Stating the Problem
- 1.1.2 Solving the Problem
- 1.1.3 Generalizing the Problem and Solution: Efficiencies
- 1.1.4 Numerical Test
- 1.2 From Shooting Hoops to the Geometric Series
- 1.2.1 The Problem and Its Solution
- 1.2.2 Related Problems
- 1.2.3 General Problem Solving Tips
- 1.3 Gambling
- 1.3.1 The 2008 Super Bowl Wager
- 1.3.2 Expected Returns
- 1.3.3 The Value of Hedging
- 1.3.4 Consequences
- 1.4 Summary
- 1.5 Exercises
- 1.1 Birthday Problem
- 2 Basic Probability Laws
- 2.1 Paradoxes
- 2.2 Set Theory Review
- 2.2.1 Coding Digression
- 2.2.2 Sizes of Infinity and Probabilities
- 2.2.3 Open and Closed Sets
- 2.3 Outcome Spaces, Events, and the Axioms of Probability
- 2.4 Axioms of Probability
- 2.5 Basic Probability Rules
- 2.5.1 Law of Total Probability
- 2.5.2 Probabilities of Unions
- 2.5.3 Probabilities of Inclusions
- 2.6 Probability Spaces and σ-algebras
- 2.7 Appendix: Experimentally Finding Formulas
- 2.7.1 Product Rule for Derivatives
- 2.7.2 Probability of a Union
- 2.8 Summary
- 2.9 Exercises
- 3 Counting I: Cards
- 3.1 Factorials and Binomial Coefficients
- 3.1.1 The Factorial Function
- 3.1.2 Binomial Coefficients
- 3.1.3 Summary
- 3.2 Poker
- 3.2.1 Rules
- 3.2.2 Nothing
- 3.2.3 Pair
- 3.2.4 Two Pair
- 3.2.5 Three of a Kind
- 3.2.6 Straights, Flushes, and Straight Flushes
- 3.2.7 Full House and Four of a Kind
- 3.2.8 Practice Poker Hand: I
- 3.2.9 Practice Poker Hand: II
- 3.3 Solitaire
- 3.3.1 Klondike
- 3.3.2 Aces Up
- 3.3.3 FreeCell
- 3.4 Bridge
- 3.4.1 Tic-tac-toe
- 3.4.2 Number of Bridge Deals
- 3.4.3 Trump Splits
- 3.5 Appendix: Coding to Compute Probabilities
- 3.5.1 Trump Split and Code
- 3.5.2 Poker Hand Codes
- 3.6 Summary
- 3.7 Exercises
- 3.1 Factorials and Binomial Coefficients
- 4 Conditional Probability, Independence, and Bayes’ Theorem
- 4.1 Conditional Probabilities
- 4.1.1 Guessing the Conditional Probability Formula
- 4.1.2 Expected Counts Approach
- 4.1.3 Venn Diagram Approach
- 4.1.4 The Monty Hall Problem
- 4.2 The General Multiplication Rule
- 4.2.1 Statement
- 4.2.2 Poker Example
- 4.2.3 Hat Problem and Error Correcting Codes
- 4.2.4 Advanced Remark: Definition of Conditional Probability
- 4.3 Independence
- 4.4 Bayes’ Theorem
- 4.5 Partitions and the Law of Total Probability
- 4.6 Bayes’ Theorem Revisited
- 4.7 Summary
- 4.8 Exercises
- 4.1 Conditional Probabilities
- 5 Counting II: Inclusion-Exclusion
- 5.1 Factorial and Binomial Problems
- 5.1.1 “How many” versus “What’s the probability”
- 5.1.2 Choosing Groups
- 5.1.3 Circular Orderings
- 5.1.4 Choosing Ensembles
- 5.2 The Method of Inclusion-Exclusion
- 5.2.1 Special Cases of the Inclusion-Exclusion Principle
- 5.2.2 Statement of the Inclusion-Exclusion Principle
- 5.2.3 Justification of the Inclusion-Exclusion Formula
- 5.2.4 Using Inclusion-Exclusion: Suited Hand
- 5.2.5 The At Least to Exactly Method
- 5.3 Derangements
- 5.3.1 Counting Derangements
- 5.3.2 The Probability of a Derangement
- 5.3.3 Coding Derangement Experiments
- 5.3.4 Applications of Derangements
- 5.4 Summary
- 5.5 Exercises
- 5.1 Factorial and Binomial Problems
- 6 Counting III: Advanced Combinatorics
- 6.1 Basic Counting
- 6.1.1 Enumerating Cases: I
- 6.1.2 Enumerating Cases: II
- 6.1.3 Sampling With and Without Replacement
- 6.2 Word Orderings
- 6.2.1 Counting Orderings
- 6.2.2 Multinomial Coefficients
- 6.3 Partitions
- 6.3.1 The Cookie Problem
- 6.3.2 Lotteries
- 6.3.3 Additional Partitions
- 6.4 Summary
- 6.5 Exercises
- 6.1 Basic Counting
- 1 Introduction
- II Introduction to Random Variables
- 7 Introduction to Discrete Random Variables
- 7.1 Discrete Random Variables: Definition
- 7.2 Discrete Random Variables: PDFs
- 7.3 Discrete Random Variables: CDFs
- 7.4 Summary
- 7.5 Exercises
- 8 Introduction to Continuous Random Variables
- 8.1 Fundamental Theorem of Calculus
- 8.2 PDFs and CDFs: Definitions
- 8.3 PDFs and CDFs: Examples
- 8.4 Probabilities of Singleton Events
- 8.5 Summary
- 8.6 Exercises
- 9 Tools: Expectation
- 9.1 Calculus Motivation
- 9.2 Expected Values and Moments
- 9.3 Mean and Variance
- 9.4 Joint Distributions
- 9.5 Linearity of Expectation
- 9.6 Properties of the Mean and the Variance
- 9.7 Skewness and Kurtosis
- 9.8 Covariances
- 9.9 Summary
- 9.10 Exercises
- 10 Tools: Convolutions and Changing Variables
- 10.1 Convolutions: Definitions and Properties
- 10.2 Convolutions: Die Example
- 10.2.1 Theoretical Calculation
- 10.2.2 Convolution Code
- 10.3 Convolutions of Several Variables
- 10.4 Change of Variable Formula: Statement
- 10.5 Change of Variables Formula: Proof
- 10.6 Appendix: Products and Quotients of Random Variables
- 10.6.1 Density of a Product
- 10.6.2 Density of a Quotient
- 10.6.3 Example: Quotient of Exponentials
- 10.7 Summary
- 10.8 Exercises
- 11 Tools: Differentiating Identities
- 11.1 Geometric Series Example
- 11.2 Method of Differentiating Identities
- 11.3 Applications to Binomial Random Variables
- 11.4 Applications to Normal Random Variables
- 11.5 Applications to Exponential Random Variables
- 11.6 Summary
- 11.7 Exercises
- 7 Introduction to Discrete Random Variables
- III Special Distributions
- 12 Discrete Distributions
- 12.1 The Bernoulli Distribution
- 12.2 The Binomial Distribution
- 12.3 The Multinomial Distribution
- 12.4 The Geometric Distribution
- 12.5 The Negative Binomial Distribution
- 12.6 The Poisson Distribution
- 12.7 The Discrete Uniform Distribution
- 12.8 Exercises
- 13 Continuous Random Variables: Uniform and Exponential
- 13.1 The Uniform Distribution
- 13.1.1 Mean and Variance
- 13.1.2 Sums of Uniform Random Variables
- 13.1.3 Examples
- 13.1.4 Generating Random Numbers Uniformly
- 13.2 The Exponential Distribution
- 13.2.1 Mean and Variance
- 13.2.2 Sums of Exponential Random Variables
- 13.2.3 Examples and Applications of Exponential Random Variables
- 13.2.4 Generating Random Numbers from Exponential Distributions
- 13.3 Exercises
- 13.1 The Uniform Distribution
- 14 Continuous Random Variables: The Normal Distribution
- 14.1 Determining the Normalization Constant
- 14.2 Mean and Variance
- 14.3 Sums of Normal Random Variables
- 14.3.1 Case 1: μX = μY = 0 and 2/x = 2/y = 1
- 14.3.2 Case 2: General μX, μY and 2/x, 2/y
- 14.3.3 Sums of Two Normals: Faster Algebra
- 14.4 Generating Random Numbers from Normal Distributions
- 14.5 Examples and the Central Limit Theorem
- 14.6 Exercises
- 15 The Gamma Function and Related Distributions
- 15.1 Existence of Γ (s)
- 15.2 The Functional Equation of Γ (s)
- 15.3 The Factorial Function and Γ (s)
- 15.4 Special Values of Γ (s)
- 15.5 The Beta Function and the Gamma Function
- 15.5.1 Proof of the Fundamental Relation
- 15.5.2 The Fundamental Relation and Γ(1/2)
- 15.6 The Normal Distribution and the Gamma Function
- 15.7 Families of Random Variables
- 15.8 Appendix: Cosecant Identity Proofs
- 15.8.1 The Cosecant Identity: First Proof
- 15.8.2 The Cosecant Identity: Second Proof
- 15.8.3 The Cosecant Identity: Special Case s = 1/2
- 15.9 Cauchy Distribution
- 15.10 Exercises
- 16 The Chi-square Distribution
- 16.1 Origin of the Chi-square Distribution
- 16.2 Mean and Variance of X ∼ χ2(1)
- 16.3 Chi-square Distributions and Sums of Normal Random Variables
- 16.3.1 Sums of Squares by Direct Integration
- 16.3.2 Sums of Squares by the Change of Variables Theorem
- 16.3.3 Sums of Squares by Convolution
- 16.3.4 Sums of Chi-square Random Variables
- 16.4 Summary
- 16.5 Exercises
- 12 Discrete Distributions
- IV Limit Theorems
- 17 Inequalities and Laws of Large Numbers
- 17.1 Inequalities
- 17.2 Markov’s Inequality
- 17.3 Chebyshev’s Inequality
- 17.3.1 Statement
- 17.3.2 Proof
- 17.3.3 Normal and Uniform Examples
- 17.3.4 Exponential Example
- 17.4 The Boole and Bonferroni Inequalities
- 17.5 Types of Convergence
- 17.5.1 Convergence in Distribution
- 17.5.2 Convergence in Probability
- 17.5.3 Almost Sure and Sure Convergence
- 17.6 Weak and Strong Laws of Large Numbers
- 17.7 Exercises
- 18 Stirling’s Formula
- 18.1 Stirling’s Formula and Probabilities
- 18.2 Stirling’s Formula and Convergence of Series
- 18.3 From Stirling to the Central Limit Theorem
- 18.4 Integral Test and the Poor Man’s Stirling
- 18.5 Elementary Approaches towards Stirling’s Formula
- 18.5.1 Dyadic Decompositions
- 18.5.2 Lower Bounds towards Stirling: I
- 18.5.3 Lower Bounds toward Stirling II
- 18.5.4 Lower Bounds towards Stirling: III
- 18.6 Stationary Phase and Stirling
- 18.7 The Central Limit Theorem and Stirling
- 18.8 Exercises
- 19 Generating Functions and Convolutions
- 19.1 Motivation
- 19.2 Definition
- 19.3 Uniqueness and Convergence of Generating Functions
- 19.4 Convolutions I: Discrete Random Variables
- 19.5 Convolutions II: Continuous Random Variables
- 19.6 Definition and Properties of Moment Generating Functions
- 19.7 Applications of Moment Generating Functions
- 19.8 Exercises
- 20 Proof of the Central Limit Theorem
- 20.1 Key Ideas of the Proof
- 20.2 Statement of the Central Limit Theorem
- 20.3 Means, Variances, and Standard Deviations
- 20.4 Standardization
- 20.5 Needed Moment Generating Function Results
- 20.6 Special Case: Sums of Poisson Random Variables
- 20.7 Proof of the CLT for General Sums via MGF
- 20.8 Using the Central Limit Theorem
- 20.9 The Central Limit Theorem and Monte Carlo Integration
- 20.10 Summary
- 20.11 Exercises
- 21 Fourier Analysis and the Central Limit Theorem
- 21.1 Integral Transforms
- 21.2 Convolutions and Probability Theory
- 21.3 Proof of the Central Limit Theorem
- 21.4 Summary
- 21.5 Exercises
- 17 Inequalities and Laws of Large Numbers
- V Additional Topics
- 22 Hypothesis Testing
- 22.1 Z-tests
- 22.1.1 Null and Alternative Hypotheses
- 22.1.2 Significance Levels
- 22.1.3 Test Statistics
- 22.1.4 One-sided versus Two-sided Tests
- 22.2 On p-values
- 22.2.1 Extraordinary Claims and p-values
- 22.2.2 Large p-values
- 22.2.3 Misconceptions about p-values
- 22.3 On t-tests
- 22.3.1 Estimating the Sample Variance
- 22.3.2 From z-tests to t-tests
- 22.4 Problems with Hypothesis Testing
- 22.4.1 Type I Errors
- 22.4.2 Type II Errors
- 22.4.3 Error Rates and the Justice System
- 22.4.4 Power
- 22.4.5 Effect Size
- 22.5 Chi-square Distributions, Goodness of Fit
- 22.5.1 Chi-square Distributions and Tests of Variance
- 22.5.2 Chi-square Distributions and t-distributions
- 22.5.3 Goodness of Fit for List Data
- 22.6 Two Sample Tests
- 22.6.1 Two-sample z-test: Known Variances
- 22.6.2 Two-sample t-test: Unknown but Same Variances
- 22.6.3 Unknown and Different Variances
- 22.7 Summary
- 22.8 Exercises
- 22.1 Z-tests
- 23 Difference Equations, Markov Processes, and Probability
- 23.1 From the Fibonacci Numbers to Roulette
- 23.1.1 The Double-plus-one Strategy
- 23.1.2 A Quick Review of the Fibonacci Numbers
- 23.1.3 Recurrence Relations and Probability
- 23.1.4 Discussion and Generalizations
- 23.1.5 Code for Roulette Problem
- 23.2 General Theory of Recurrence Relations
- 23.2.1 Notation
- 23.2.2 The Characteristic Equation
- 23.2.3 The Initial Conditions
- 23.2.4 Proof that Distinct Roots Imply Invertibility
- 23.3 Markov Processes
- 23.3.1 Recurrence Relations and Population Dynamics
- 23.3.2 General Markov Processes
- 23.4 Summary
- 23.5 Exercises
- 23.1 From the Fibonacci Numbers to Roulette
- 24 The Method of Least Squares
- 24.1 Description of the Problem
- 24.2 Probability and Statistics Review
- 24.3 The Method of Least Squares
- 24.4 Exercises
- 25 Two Famous Problems and Some Coding
- 25.1 The Marriage/Secretary Problem
- 25.1.1 Assumptions and Strategy
- 25.1.2 Probability of Success
- 25.1.3 Coding the Secretary Problem
- 25.2 Monty Hall Problem
- 25.2.1 A Simple Solution
- 25.2.2 An Extreme Case
- 25.2.3 Coding the Monty Hall Problem
- 25.3 Two Random Programs
- 25.3.1 Sampling with and without Replacement
- 25.3.2 Expectation
- 25.4 Exercises
- 25.1 The Marriage/Secretary Problem
- Appendix A Proof Techniques
- A.1 How to Read a Proof
- A.2 Proofs by Induction
- A.2.1 Sums of Integers
- A.2.2 Divisibility
- A.2.3 The Binomial Theorem
- A.2.4 Fibonacci Numbers Modulo 2
- A.2.5 False Proofs by Induction
- A.3 Proof by Grouping
- A.4 Proof by Exploiting Symmetries
- A.5 Proof by Brute Force
- A.6 Proof by Comparison or Story
- A.7 Proof by Contradiction
- A.8 Proof by Exhaustion (or Divide and Conquer)
- A.9 Proof by Counterexample
- A.10 Proof by Generalizing Example
- A.11 Dirichlet’s Pigeon-Hole Principle
- A.12 Proof by Adding Zero or Multiplying by One
- Appendix B Analysis Results
- B.1 The Intermediate and Mean Value Theorems
- B.2 Interchanging Limits, Derivatives, and Integrals
- B.2.1 Interchanging Orders: Theorems
- B.2.2 Interchanging Orders: Examples
- B.3 Convergence Tests for Series
- B.4 Big-Oh Notation
- B.5 The Exponential Function
- B.6 Proof of the Cauchy-Schwarz Inequality
- B.7 Exercises
- Appendix C Countable and Uncountable Sets
- C.1 Sizes of Sets
- C.2 Countable Sets
- C.3 Uncountable Sets
- C.4 Length of the Rationals
- C.5 Length of the Cantor Set
- C.6 Exercises
- Appendix D Complex Analysis and the Central Limit Theorem
- D.1 Warnings from Real Analysis
- D.2 Complex Analysis and Topology Definitions
- D.3 Complex Analysis and Moment Generating Functions
- D.4 Exercises
- 22 Hypothesis Testing
- Bibliography
- Index
"I recommend the book to everyone who is studying and fascinated by statistics."—Singalakha Menziwa, Mathemafrica
"Steven J. Miller’s The Probability Lifesaver presents, as its subtitle claims, 'all the tools you need to understand chance' in a clear, straightforward manner. . . . For the students that have a good understanding of Calculus, the combination of the probability discussions along with the calculus behind these topics is very beneficial."—MAA Reviews
"The breadth of the book’s coverage and its clear, informal tone in addressing highly formal problems remind one of a friendly professor offering unlimited office hours, and the book will be a highly accessible supplement for students working through another, more conventional text. . . . [This is] a volume that deserves to be widely known in educational circles and will likely find its way to the shelves of practicing statisticians who wish to probe below the surface of fundamental theorems that they have learned by rote."—H. Van Dyke Parunak, Computing Reviews
"This is a superb book by a gifted writer and mathematician. Miller's amiable, intuitive writing style weaves stories about probability into the narrative in a unique fashion."—Larry Leemis, College of William & Mary
"The Probability Lifesaver creates a wonderful mathematical experience. It combines important theories with fun problems, giving a new and creative perspective on probability. This book helped me understand the big questions behind the mathematics of probability: why the complex theories I was learning are true, where they come from, and what are their applications. This approach is a welcome complement to other heavy theoretical books, and was detailed and expansive enough to serve as the main textbook for our class."—Alexandre Gueganic, Williams College ‘19
"This fun book gives readers the feeling that they are having a live conversation with the author. A wonderful resource for students and teachers alike, The Probability Lifesaver contains clear and detailed explanations, problems with solutions on every topic, and extremely helpful background material."—Iddo Ben-Ari, University of Connecticut
"In The Probability Lifesaver, Miller does more than simply present the theoretical framework of probability. He takes complex concepts and describes them in understandable language, provides realistic applications that highlight the far-extending reaches of probability, and engages the problem-solving intuitions that lie at the heart of mathematics. Lastly, and most importantly, I am reminded throughout this textbook of why I chose to study mathematics: because it's fun!"—Michael Stone, Williams College ‘16
"The Probability Lifesaver motivates introductory probability theory with concrete applications in an approachable and engaging manner. From computing the probability of various poker hands to defining sigma-algebras, it strikes a balance between applied computation and mathematical theory that makes it easy to follow while still being mathematically satisfying."—David Burt, Williams College ‘17
"A balanced mix of theoretical and practical problem-solving approaches in probability—suited for personal study as well as textbook reading in and out of the classroom. After college, while working, I took a probability class remotely and with this book, I was able to follow easily despite being without a TA or easy access to the professor. From research examples to interview questions, it has saved my life more than once."—Dan Zhao, Williams College ‘ 14
"The Probability Lifesaver helped me build a foundation of probability theory and an appreciation for its nuances through engaging examples and easy-to-follow explanations. This well-written and extensive book will serve as your guide to probability and reward you for the time you give it."—Jaclyn Porfilio, Williams '15
"I see a tremendous value in this fun, engaging, and informal book. It has a conversational tone, which invites students to engage the material and concepts. It is as if Miller is there, lecturing on the topics, helping students to think things through for themselves."—John Imbrie, University of Virginia
"The Probability Lifesaver contains a lot of explanations and examples and provides step-by-step instructions to how definitions and ideas are formulated. I appreciated that it tries to provide multiple solutions to each problem. Interesting, informative, approachable, and comprehensive, this book was easy to read and would make a good supplement for a first probability course at the undergraduate level."—Jingchen Hu, Vassar College
"Filled with many interesting and contemporary examples, The Probability Lifesaver would have undoubtedly helped me while I was taking statistics. Miller offers careful, detailed explanations in simple terms that are easy to understand."—James Coyle, former student at Rutgers University