For many students, calculus can be the most mystifying and frustrating course they will ever take. The Calculus Lifesaver provides students with the essential tools they need not only to learn calculus, but to excel at it.
All of the material in this user-friendly study guide has been proven to get results. The book arose from Adrian Banner’s popular calculus review course at Princeton University, which he developed especially for students who are motivated to earn A’s but get only average grades on exams. The complete course will be available for free on the Web in a series of videotaped lectures. This study guide works as a supplement to any single-variable calculus course or textbook. Coupled with a selection of exercises, the book can also be used as a textbook in its own right. The style is informal, non-intimidating, and even entertaining, without sacrificing comprehensiveness. The author elaborates standard course material with scores of detailed examples that treat the reader to an “inner monologue”—the train of thought students should be following in order to solve the problem—providing the necessary reasoning as well as the solution. The book’s emphasis is on building problem-solving skills. Examples range from easy to difficult and illustrate the in-depth presentation of theory.
The Calculus Lifesaver combines ease of use and readability with the depth of content and mathematical rigor of the best calculus textbooks. It is an indispensable volume for any student seeking to master calculus.
- Serves as a companion to any single-variable calculus textbook
- Informal, entertaining, and not intimidating
- Informative videos that follow the book—a full forty-eight hours of Banner’s Princeton calculus-review course—is available at Adrian Banner lectures
- More than 475 examples (ranging from easy to hard) provide step-by-step reasoning
- Theorems and methods justified and connections made to actual practice
- Difficult topics such as improper integrals and infinite series covered in detail
- Tried and tested by students taking freshman calculus
Adrian Banner is Lecturer in Mathematics at Princeton University and Director of Research at INTECH.
- Welcome
- How to Use This Book to Study for an Exam
- Two all-purpose study tips
- Key sections for exam review (by topic)
- Acknowledgments
- 1 Functions, Graphs, and Lines
- 1.1 Functions
- 1.1.1 Interval notation
- 1.1.2 Finding the domain
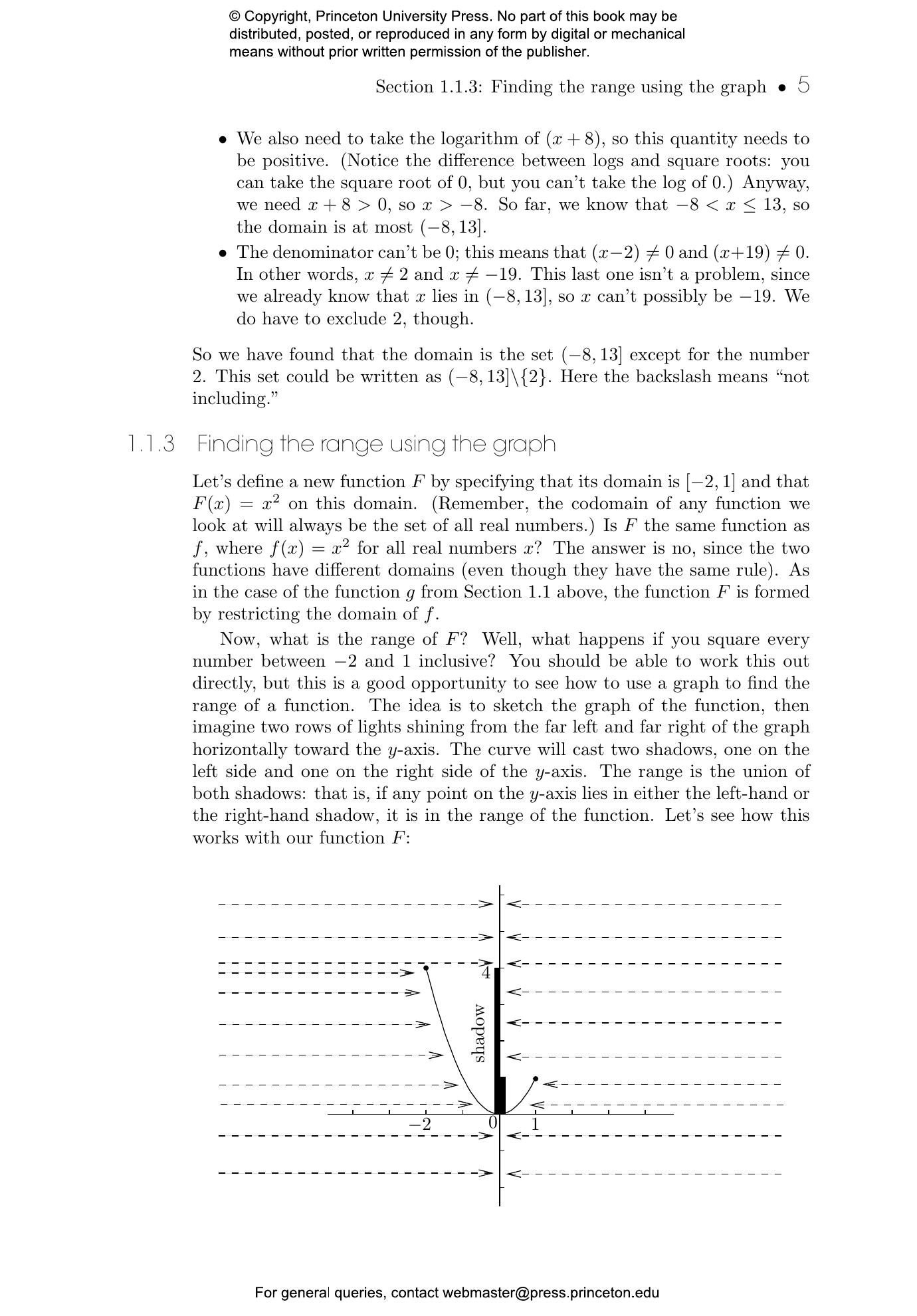
- 1.1.3 Finding the range using the graph
- 1.1.4 The vertical line test
- 1.2 Inverse Functions
- 1.2.1 The horizontal line test
- 1.2.2 Finding the inverse
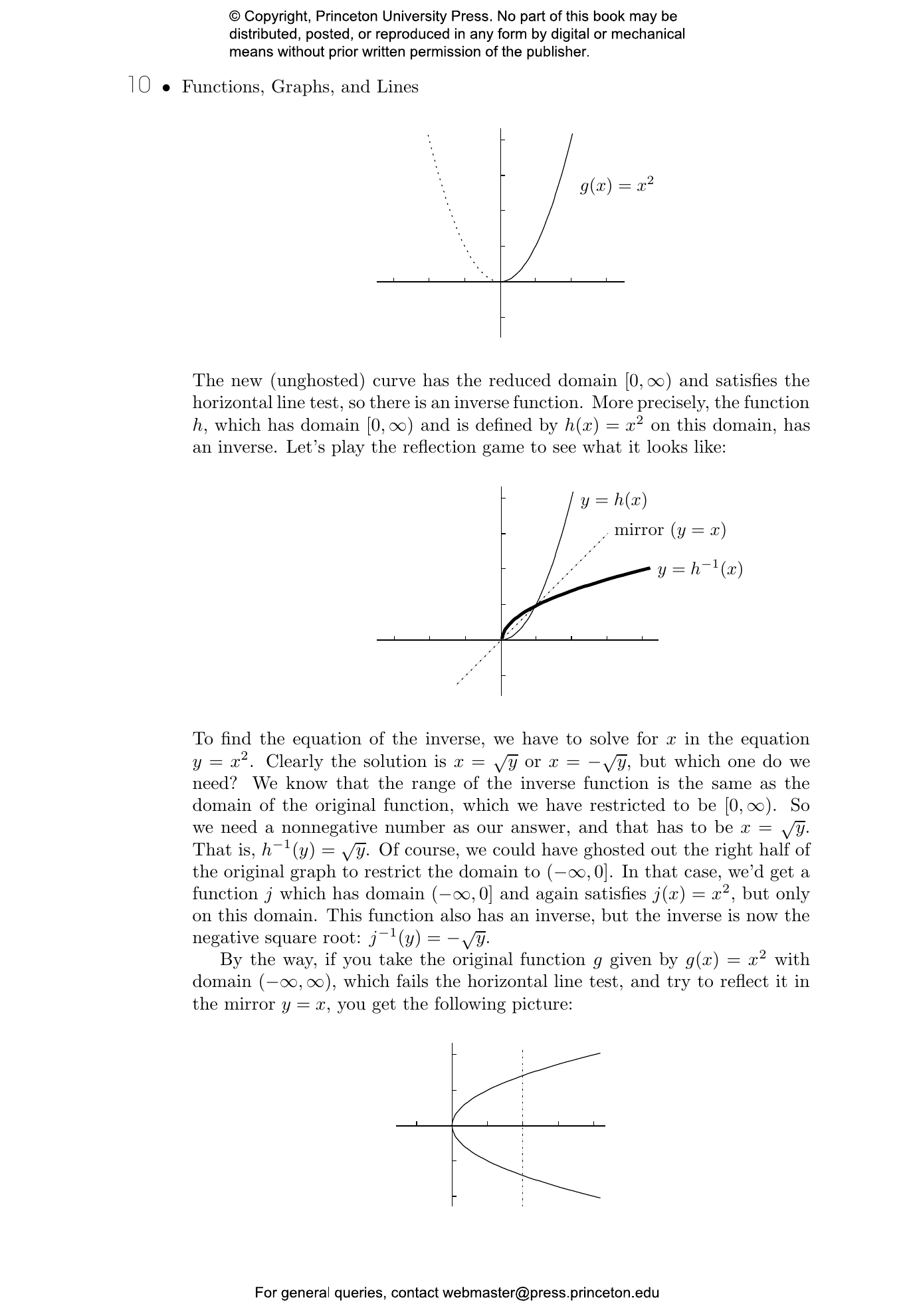
- 1.2.3 Restricting the domain
- 1.2.4 Inverses of inverse functions
- 1.3 Composition of Functions
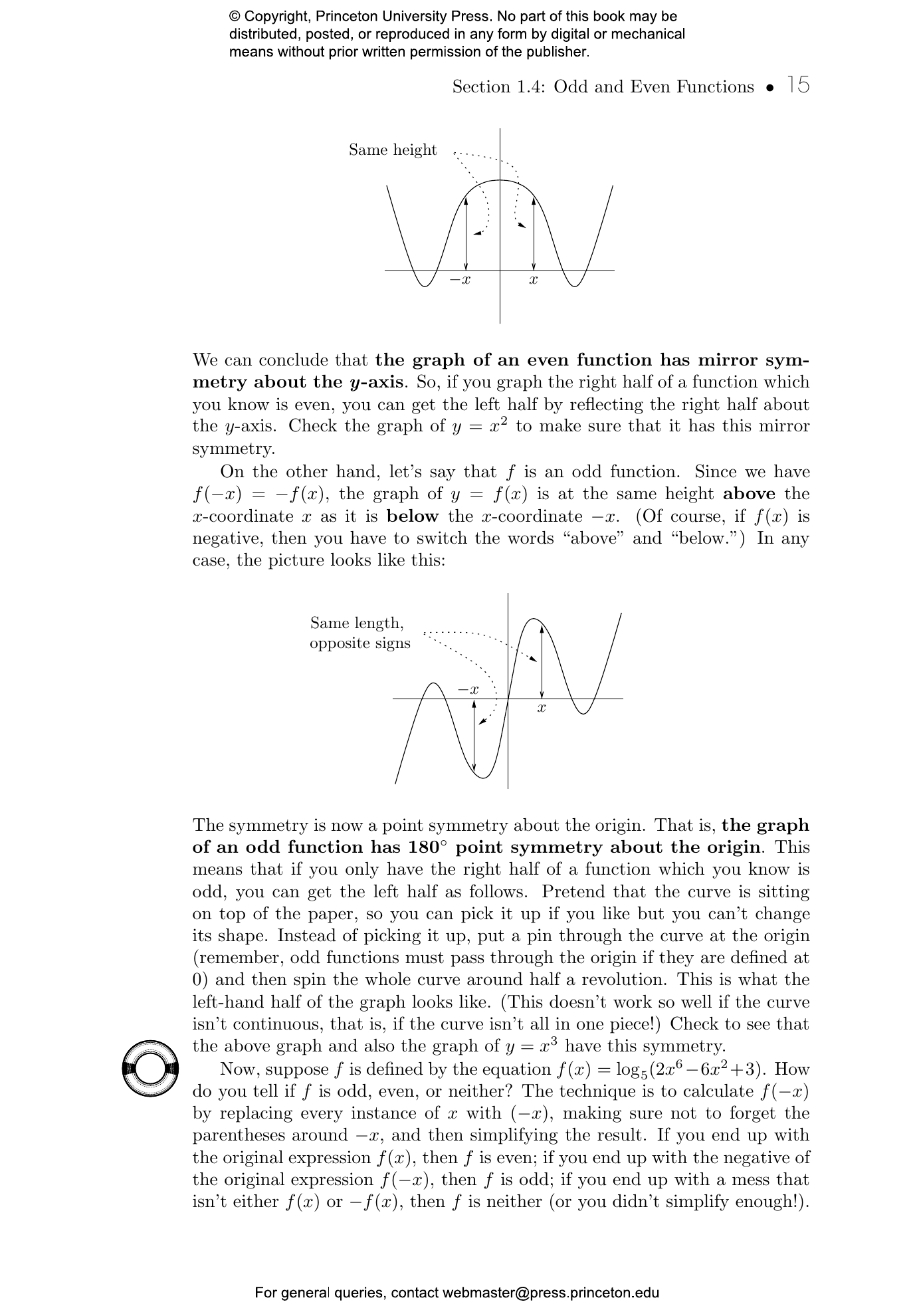
- 1.4 Odd and Even Functions
- 1.5 Graphs of Linear Functions
- 1.6 Common Functions and Graphs
- 2 Review of Trigonometry
- 2.1 The Basics
- 2.2 Extending the Domain of Trig Functions
- 2.2.1 The ASTC method
- 2.2.2 Trig functions outside [0, 2π]
- 2.3 The Graphs of Trig Functions
- 2.4 Trig Identities
- 3 Introduction to Limits
- 3.1 Limits: The Basic Idea
- 3.2 Left-Hand and Right-Hand Limits
- 3.3 When the Limit Does Not Exist
- 3.4 Limits at ∞ and −∞
- 3.4.1 Large numbers and small numbers
- 3.5 Two Common Misconceptions about Asymptotes
- 3.6 The Sandwich Principle
- 3.7 Summary of Basic Types of Limits
- 4 How to Solve Limit Problems Involving Polynomials
- 4.1 Limits Involving Rational Functions as x → a
- 4.2 Limits Involving Square Roots as x → a
- 4.3 Limits Involving Rational Functions as x → ∞
- 4.3.1 Method and examples
- 4.4 Limits Involving Poly-type Functions as x → ∞
- 4.5 Limits Involving Rational Functions as x → −∞
- 4.6 Limits Involving Absolute Values
- 5 Continuity and Differentiability
- 5.1 Continuity
- 5.1.1 Continuity at a point
- 5.1.2 Continuity on an interval
- 5.1.3 Examples of continuous functions
- 5.1.4 The Intermediate Value Theorem
- 5.1.5 A harder IVT example
- 5.1.6 Maxima and minima of continuous functions
- 5.2 Differentiability
- 5.2.1 Average speed
- 5.2.2 Displacement and velocity
- 5.2.3 Instantaneous velocity
- 5.2.4 The graphical interpretation of velocity
- 5.2.5 Tangent lines
- 5.2.6 The derivative function
- 5.2.7 The derivative as a limiting ratio
- 5.2.8 The derivative of linear functions
- 5.2.9 Second and higher-order derivatives
- 5.2.10 When the derivative does not exist
- 5.2.11 Differentiability and continuity
- 6 How to Solve Differentiation Problems
- 6.1 Finding Derivatives Using the Definition
- 6.2 Finding Derivatives (the Nice Way)
- 6.2.1 Constant multiples of functions
- 6.2.2 Sums and differences of functions
- 6.2.3 Products of functions via the product rule
- 6.2.4 Quotients of functions via the quotient rule
- 6.2.5 Composition of functions via the chain rule
- 6.2.6 A nasty example
- 6.2.7 Justification of the product rule and the chain rule
- 6.3 Finding the Equation of a Tangent Line
- 6.4 Velocity and Acceleration
- 6.4.1 Constant negative acceleration
- 6.5 Limits Which Are Derivatives in Disguise
- 6.6 Derivatives of Piecewise-Defined Functions
- 6.7 Sketching Derivative Graphs Directly
- 7 Trig Limits and Derivatives
- 7.1 Limits Involving Trig Functions
- 7.1.1 The small case
- 7.1.2 Solving problems—the small case
- 7.1.3 The large case
- 7.1.4 The “other” case
- 7.1.5 Proof of an important limit
- 7.2 Derivatives Involving Trig Functions
- 7.2.1 Examples of differentiating trig functions
- 7.2.2 Simple harmonic motion
- 7.2.3 A curious function
- 8 Implicit Differentiation and Related Rates
- 8.1 Implicit Differentiation
- 8.1.1 Techniques and examples
- 8.1.2 Finding the second derivative implicitly
- 8.2 Related Rates
- 8.2.1 A simple example
- 8.2.2 A slightly harder example
- 8.2.3 A much harder example
- 8.2.4 A really hard example
- 9 Exponentials and Logarithms
- 9.1 The Basics
- 9.1.1 Review of exponentials
- 9.1.2 Review of logarithms
- 9.1.3 Logarithms, exponentials, and inverses
- 9.1.4 Log rules
- 9.2 Definition of e
- 9.2.1 A question about compound interest
- 9.2.2 The answer to our question
- 9.2.3 More about e and logs
- 9.3 Differentiation of Logs and Exponentials
- 9.3.1 Examples of differentiating exponentials and logs
- 9.4 How to Solve Limit Problems Involving Exponentials or Logs
- 9.4.1 Limits involving the definition of e
- 9.4.2 Behavior of exponentials near 0
- 9.4.3 Behavior of logarithms near 1
- 9.4.4 Behavior of exponentials near ∞ or −∞
- 9.4.5 Behavior of logs near ∞
- 9.4.6 Behavior of logs near 0
- 9.5 Logarithmic Differentiation
- 9.5.1 The derivative of xa
- 9.6 Exponential Growth and Decay
- 9.6.1 Exponential growth
- 9.6.2 Exponential decay
- 9.7 Hyperbolic Functions
- 10 Inverse Functions and Inverse Trig Functions
- 10.1 The Derivative and Inverse Functions
- 10.1.1 Using the derivative to show that an inverse exists
- 10.1.2 Derivatives and inverse functions: what can go wrong
- 10.1.3 Finding the derivative of an inverse function
- 10.1.4 A big example
- 10.2 Inverse Trig Functions
- 10.2.1 Inverse sine
- 10.2.2 Inverse cosine
- 10.2.3 Inverse tangent
- 10.2.4 Inverse secant
- 10.2.5 Inverse cosecant and inverse cotangent
- 10.2.6 Computing inverse trig functions
- 10.3 Inverse Hyperbolic Functions
- 10.3.1 The rest of the inverse hyperbolic functions
- 11 The Derivative and Graphs
- 11.1 Extrema of Functions
- 11.1.1 Global and local extrema
- 11.1.2 The Extreme Value Theorem
- 11.1.3 How to find global maxima and minima
- 11.2 Rolle’s Theorem
- 11.3 The Mean Value Theorem
- 11.3.1 Consequences of the Mean Value Theorem
- 11.4 The Second Derivative and Graphs
- 11.4.1 More about points of inflection
- 11.5 Classifying Points Where the Derivative Vanishes
- 11.5.1 Using the first derivative
- 11.5.2 Using the second derivative
- 12 Sketching Graphs
- 12.1 How to Construct a Table of Signs
- 12.1.1 Making a table of signs for the derivative
- 12.1.2 Making a table of signs for the second derivative
- 12.2 The Big Method
- 12.3 Examples
- 12.3.1 An example without using derivatives
- 12.3.2 The full method: example 1
- 12.3.3 The full method: example 2
- 12.3.4 The full method: example 3
- 12.3.5 The full method: example 4
- 13 Optimization and Linearization
- 13.1 Optimization
- 13.1.1 An easy optimization example
- 13.1.2 Optimization problems: the general method
- 13.1.3 An optimization example
- 13.1.4 Another optimization example
- 13.1.5 Using implicit differentiation in optimization
- 13.1.6 A difficult optimization example
- 13.2 Linearization
- 13.2.1 Linearization in general
- 13.2.2 The differential
- 13.2.3 Linearization summary and examples
- 13.2.4 The error in our approximation
- 13.3 Newton’s Method
- 14 L’Hôpital’s Rule and Overview of Limits
- 14.1 L’Hôpital’s Rule
- 14.1.1 Type A: 0/0 case
- 14.1.2 Type A: ±∞/±∞ case
- 14.1.3 Type B1 (∞ − ∞)
- 14.1.4 Type B2 (0 × ±∞)
- 14.1.5 Type C (1±∞ 00, or ∞0)
- 14.1.6 Summary of l’Hôpital’s Rule types
- 14.2 Overview of Limits
- 15 Introduction to Integration
- 15.1 Sigma Notation
- 15.1.1 A nice sum
- 15.1.2 Telescoping series
- 15.2 Displacement and Area
- 15.2.1 Three simple cases
- 15.2.2 A more general journey
- 15.2.3 Signed area
- 15.2.4 Continuous velocity
- 15.2.5 Two special approximations
- 16 Definite Integrals
- 16.1 The Basic Idea
- 16.1.1 Some easy examples
- 16.2 Definition of the Definite Integral
- 16.2.1 An example of using the definition
- 16.3 Properties of Definite Integrals
- 16.4 Finding Areas
- 16.4.1 Finding the unsigned area
- 16.4.2 Finding the area between two curves
- 16.4.3 Finding the area between a curve and the y-axis
- 16.5 Estimating Integrals
- 16.5.1 A simple type of estimation
- 16.6 Averages and the Mean Value Theorem for Integrals
- 16.6.1 The Mean Value Theorem for integrals
- 16.7 A Nonintegrable Function
- 17 The Fundamental Theorems of Calculus
- 17.1 Functions Based on Integrals of Other Functions
- 17.2 The First Fundamental Theorem
- 17.2.1 Introduction to antiderivatives
- 17.3 The Second Fundamental Theorem
- 17.4 Indefinite Integrals
- 17.5 How to Solve Problems: The First Fundamental Theorem
- 17.5.1 Variation 1: variable left-hand limit of integration
- 17.5.2 Variation 2: one tricky limit of integration
- 17.5.3 Variation 3: two tricky limits of integration
- 17.5.4 Variation 4: limit is a derivative in disguise
- 17.6 How to Solve Problems: The Second Fundamental Theorem
- 17.6.1 Finding indefinite integrals
- 17.6.2 Finding definite integrals
- 17.6.3 Unsigned areas and absolute values
- 17.7 A Technical Point
- 17.8 Proof of the First Fundamental Theorem
- 18 Techniques of Integration, Part One
- 18.1 Substitution
- 18.1.1 Substitution and definite integrals
- 18.1.2 How to decide what to substitute
- 18.1.3 Theoretical justification of the substitution method
- 18.2 Integration by Parts
- 18.3 Partial Fractions
- 18.3.1 The algebra of partial fractions
- 18.3.2 Integrating the pieces
- 18.3.3 The method and a big example
- 19 Techniques of Integration, Part Two
- 19.1 Integrals Involving Trig Identities
- 19.2 Integrals Involving Powers of Trig Functions
- 19.2.1 Powers of sin and/or cos
- 19.2.2 Powers of tan
- 19.2.3 Powers of sec
- 19.2.4 Powers of cot
- 19.2.5 Powers of csc
- 19.2.6 Reduction formulas
- 19.3 Integrals Involving Trig Substitutions
- 19.3.1 Type 1: √ a2−x2
- 19.3.2 Type 2: √ x2+a2
- 19.3.3 Type 3: √ x2−a2
- 19.3.4 Completing the square and trig substitutions
- 19.3.5 Summary of trig substitutions
- 19.3.6 Technicalities of square roots and trig substitutions
- 19.4 Overview of Techniques of Integration
- 20 Improper Integrals: Basic Concepts
- 20.1 Convergence and Divergence
- 20.1.1 Some examples of improper integrals
- 20.1.2 Other blow-up points
- 20.2 Integrals over Unbounded Regions
- 20.3 The Comparison Test (Theory)
- 20.4 The Limit Comparison Test (Theory)
- 20.4.1 Functions asymptotic to each other
- 20.4.2 The statement of the test
- 20.5 The p-test (Theory)
- 20.6 The Absolute Convergence Test
- 21 Improper Integrals: How to Solve Problems
- 21.1 How to Get Started
- 21.1.1 Splitting up the integral
- 21.1.2 How to deal with negative function values
- 21.2 Summary of Integral Tests
- 21.3 Behavior of Common Functions near ∞ and −∞
- 21.3.1 Polynomials and poly-type functions near ∞ and −∞
- 21.3.2 Trig functions near ∞ and −∞
- 21.3.3 Exponentials near ∞ and −∞
- 21.3.4 Logarithms near ∞
- 21.4 Behavior of Common Functions near 0
- 21.4.1 Polynomials and poly-type functions near 0
- 21.4.2 Trig functions near 0
- 21.4.3 Exponentials near 0
- 21.4.4 Logarithms near 0
- 21.4.5 The behavior of more general functions near 0
- 21.5 How to Deal with Problem Spots Not at 0 or ∞
- 22 Sequences and Series: Basic Concepts
- 22.1 Convergence and Divergence of Sequences
- 22.1.1 The connection between sequences and functions
- 22.1.2 Two important sequences
- 22.2 Convergence and Divergence of Series
- 22.2.1 Geometric series (theory)
- 22.3 The nth Term Test (Theory)
- 22.4 Properties of Both Infinite Series and Improper Integrals
- 22.4.1 The comparison test (theory)
- 22.4.2 The limit comparison test (theory)
- 22.4.3 The p-test (theory)
- 22.4.4 The absolute convergence test
- 22.5 New Tests for Series
- 22.5.1 The ratio test (theory)
- 22.5.2 The root test (theory)
- 22.5.3 The integral test (theory)
- 22.5.4 The alternating series test (theory)
- 23 How to Solve Series Problems
- 23.1 How to Evaluate Geometric Series
- 23.2 How to Use the nth Term Test
- 23.3 How to Use the Ratio Test
- 23.4 How to Use the Root Test
- 23.5 How to Use the Integral Test
- 23.6 Comparison Test, Limit Comparison Test, and p-test
- 23.7 How to Deal with Series with Negative Terms
- 24 Taylor Polynomials, Taylor Series, and Power Series
- 24.1 Approximations and Taylor Polynomials
- 24.1.1 Linearization revisited
- 24.1.2 Quadratic approximations
- 24.1.3 Higher-degree approximations
- 24.1.4 Taylor’s Theorem
- 24.2 Power Series and Taylor Series
- 24.2.1 Power series in general
- 24.2.2 Taylor series and Maclaurin series
- 24.2.3 Convergence of Taylor series
- 24.3 A Useful Limit
- 25 How to Solve Estimation Problems
- 25.1 Summary of Taylor Polynomials and Series
- 25.2 Finding Taylor Polynomials and Series
- 25.3 Estimation Problems Using the Error Term
- 25.3.1 First example
- 25.3.2 Second example
- 25.3.3 Third example
- 25.3.4 Fourth example
- 25.3.5 Fifth example
- 25.3.6 General techniques for estimating the error term
- 25.4 Another Technique for Estimating the Error
- 26 Taylor and Power Series: How to Solve Problems
- 26.1 Convergence of Power Series
- 26.1.1 Radius of convergence
- 26.1.2 How to find the radius and region of convergence
- 26.2 Getting New Taylor Series from Old Ones
- 26.2.1 Substitution and Taylor series
- 26.2.2 Differentiating Taylor series
- 26.2.3 Integrating Taylor series
- 26.2.4 Adding and subtracting Taylor series
- 26.2.5 Multiplying Taylor series
- 26.2.6 Dividing Taylor series
- 26.3 Using Power and Taylor Series to Find Derivatives
- 26.4 Using Maclaurin Series to Find Limits
- 27 Parametric Equations and Polar Coordinates
- 27.1 Parametric Equations
- 27.1.1 Derivatives of parametric equations
- 27.2 Polar Coordinates
- 27.2.1 Converting to and from polar coordinates
- 27.2.2 Sketching curves in polar coordinates
- 27.2.3 Finding tangents to polar curves
- 27.2.4 Finding areas enclosed by polar curves
- 28 Complex Numbers
- 28.1 The Basics
- 28.1.1 Complex exponentials
- 28.2 The Complex Plane
- 28.2.1 Converting to and from polar form
- 28.3 Taking Large Powers of Complex Numbers
- 28.4 Solving zn = w
- 28.5 Solving ez = w
- 28.6 Some Trigonometric Series
- 28.7 Euler’s Identity and Power Series
- 29 Volumes, Arc Lengths, and Surface Areas
- 29.1 Volumes of Solids of Revolution
- 29.1.1 The disc method
- 29.1.2 The shell method
- 29.1.3 Summary … and variations
- 29.1.4 Variation 1: regions between a curve and the y-axis
- 29.1.5 Variation 2: regions between two curves
- 29.1.6 Variation 3: axes parallel to the coordinate axes
- 29.2 Volumes of General Solids
- 29.3 Arc Lengths
- 29.3.1 Parametrization and speed
- 29.4 Surface Areas of Solids of Revolution
- 30 Differential Equations
- 30.1 Introduction to Differential Equations
- 30.2 Separable First-order Differential Equations
- 30.3 First-order Linear Equations
- 30.3.1 Why the integrating factor works
- 30.4 Constant-coefficient Differential Equations
- 30.4.1 Solving first-order homogeneous equations
- 30.4.2 Solving second-order homogeneous equations
- 30.4.3 Why the characteristic quadratic method works
- 30.4.4 Nonhomogeneous equations and particular solutions
- 30.4.5 Finding a particular solution
- 30.4.6 Examples of finding particular solutions
- 30.4.7 Resolving conflicts between yP and yH
- 30.4.8 Initial value problems (constant-coefficient linear)
- 30.5 Modeling Using Differential Equations
- Appendix A Limits and Proofs
- A.1 Formal Definition of a Limit
- A.1.1 A little game
- A.1.2 The actual definition
- A.1.3 Examples of using the definition
- A.2 Making New Limits from Old Ones
- A.2.1 Sums and differences of limits—proofs
- A.2.2 Products of limits—proof
- A.2.3 Quotients of limits—proof
- A.2.4 The sandwich principle—proof
- A.3 Other Varieties of Limits
- A.3.1 Infinite limits
- A.3.2 Left-hand and right-hand limits
- A.3.3 Limits at ∞ and −∞
- A.3.4 Two examples involving trig
- A.4 Continuity and Limits
- A.4.1 Composition of continuous functions
- A.4.2 Proof of the Intermediate Value Theorem
- A.4.3 Proof of the Max-Min Theorem
- A.5 Exponentials and Logarithms Revisited
- A.6 Differentiation and Limits
- A.6.1 Constant multiples of functions
- A.6.2 Sums and differences of functions
- A.6.3 Proof of the product rule
- A.6.4 Proof of the quotient rule
- A.6.5 Proof of the chain rule
- A.6.6 Proof of the Extreme Value Theorem
- A.6.7 Proof of Rolle’s Theorem
- A.6.8 Proof of the Mean Value Theorem
- A.6.9 The error in linearization
- A.6.10 Derivatives of piecewise-defined functions
- A.6.11 Proof of l’Hôpital’s Rule
- A.7 Proof of the Taylor Approximation Theorem
- Appendix B Estimating Integrals
- B.1 Estimating Integrals Using Strips
- B.1.1 Evenly spaced partitions
- B.2 The Trapezoidal Rule
- B.3 Simpson’s Rule
- B.3.1 Proof of Simpson’s rule
- B.4 The Error in Our Approximations
- B.4.1 Examples of estimating the error
- B.4.2 Proof of an error term inequality
- List of Symbols
- Index
"Banner's style is informal, engaging and distinctly non-intimidating, and he takes pains to not skip any steps in discussing a problem. Because of its unique approach, The Calculus Lifesaver is a welcome addition to the arsenal of calculus teaching aids."—MAA Online
"This rather lengthy book serves as an excellent resource as well as a text for a refresher course in single-variable calculus, and as a study guide for anyone who needs or is required to know basic calculus concepts....Readers will find this book written for them, as calculus is presented in a very casual conversational tone; certainly, students who are not mathematics majors will benefit greatly."—J.T. Zerger, Choice
"Students who are having difficulty in calculus could use it as a resource in addition to their professor and teaching assistant."—Mathematics Teacher
"I used Adrian Banner's The Calculus Lifesaver as the sole textbook for an intensive, three-week summer Calculus I course for high-school students. I chose this book for several reasons, among them its conversational expository style, its wealth of worked-out examples, and its price. This book is designed to supplement any standard calculus textbook, thus my students will be able to use it again when they take later calculus courses. The students in my class came from diverse backgrounds, ranging from those who had already seen much of the material to others who were struggling with basic algebra. They all uniformly praised the book for being one of the clearest mathematics texts they have ever read, and because it reviews the required prerequisite material. The numerous worked-out examples are an ideal supplement to the lectures. The only difficulty in using this book as a primary text is the lack of additional exercises in the text. However, there are so many sites and sources for calculus problems that this was not a problem. I would definitely use this book again."—Steven J. Miller, Brown University
"Banner's book is a chatty, user-friendly guide to calculus that will be a useful addition to the resources available to students. Banner does an exceptionally thorough job while maintaining an engaging style."—Gerald B. Folland, author of Advanced Calculus
"This is an engaging read. Each page engenders at least one smile, often a chuckle, occasionally a belly laugh."—Charles R. MacCluer, author of Honors Calculus
"This book is significant. The author's attempt to give an 'inner monologue' into the thought process that is needed to solve calculus problems rather than just providing worked examples is novel and is in line with his purpose of helping the reader get a deeper understanding of calculus. The book is well written and the author's examples are clear and complete."—Thomas Seidenberg, Phillips Exeter Academy