Calculus is a beautiful subject that most of us learn from professors, textbooks, or supplementary texts. Each of these resources has strengths but also weaknesses. In Calculus Simplified, Oscar Fernandez combines the strengths and omits the weaknesses, resulting in a “Goldilocks approach” to learning calculus: just the right level of detail, the right depth of insights, and the flexibility to customize your calculus adventure.
Fernandez begins by offering an intuitive introduction to the three key ideas in calculus—limits, derivatives, and integrals. The mathematical details of each of these pillars of calculus are then covered in subsequent chapters, which are organized into mini-lessons on topics found in a college-level calculus course. Each mini-lesson focuses first on developing the intuition behind calculus and then on conceptual and computational mastery. Nearly 200 solved examples and more than 300 exercises allow for ample opportunities to practice calculus. And additional resources—including video tutorials and interactive graphs—are available on the book’s website.
Calculus Simplified also gives you the option of personalizing your calculus journey. For example, you can learn all of calculus with zero knowledge of exponential, logarithmic, and trigonometric functions—these are discussed at the end of each mini-lesson. You can also opt for a more in-depth understanding of topics—chapter appendices provide additional insights and detail. Finally, an additional appendix explores more in-depth real-world applications of calculus.
Learning calculus should be an exciting voyage, not a daunting task. Calculus Simplified gives you the freedom to choose your calculus experience, and the right support to help you conquer the subject with confidence.
- An accessible, intuitive introduction to first-semester calculus
- Nearly 200 solved problems and more than 300 exercises (all with answers)
- No prior knowledge of exponential, logarithmic, or trigonometric functions required
- Additional online resources—video tutorials and supplementary exercises—provided
Oscar E. Fernandez is associate professor of mathematics at Wellesley College. He is the author of Everyday Calculus and The Calculus of Happiness (both Princeton).
- Preface
- To the Student
- To the Instructor
- Before You Begin …
- 1 The Fast Track Introduction to Calculus
- 1.1 What Is Calculus?
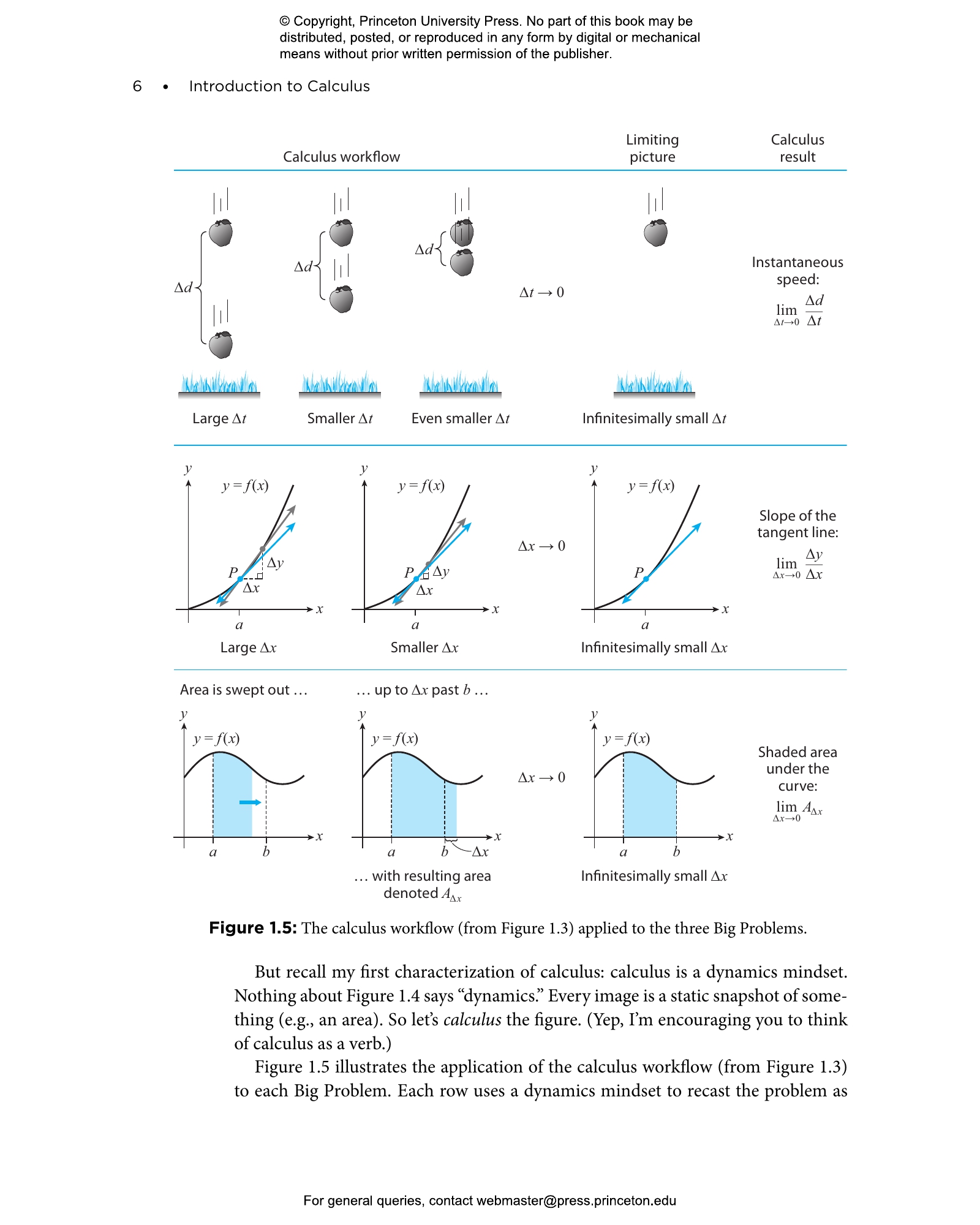
- Calculus as a Way of Thinking
- What Does “Infinitesimal Change” Mean?
- 1.2 Limits: The Foundation of Calculus
- 1.3 The Three Difficult Problems That Led to the Invention of Calculus
- 2 Limits: How to Approach Indefinitely (and Thus Never Arrive)
- 2.1 One-Sided Limits: A Graphical Approach
- 2.2 Existence of One-Sided Limits
- 2.3 Two-Sided Limits
- 2.4 Continuity at a Point
- 2.5 Continuity on an Interval
- 2.6 The Limit Laws
- 2.7 Calculating Limits—Algebraic Techniques
- 2.8 Limits Approaching Infinity
- 2.9 Limits Yielding Infinity
- 2.10 Parting Thoughts
- 3 Derivatives: Change, Quantified
- 3.1 Solving the Instantaneous Speed Problem
- 3.2 Solving the Tangent Line Problem—The Derivative at a Point
- 3.3 The Instantaneous Rate of Change Interpretation of the Derivative
- 3.4 Differentiability: When Derivatives Do (and Don’t) Exist
- 3.5 The Derivative, a Graphical Approach
- 3.6 The Derivative, an Algebraic Approach Leibniz Notation
- 3.7 Differentiation Shortcuts: The Basic Rules
- 3.8 Differentiation Shortcuts: The Power Rule
- 3.9 Differentiation Shortcuts: The Product Rule
- 3.10 Differentiation Shortcuts: The Chain Rule
- 3.11 Differentiation Shortcuts: The Quotient Rule
- 3.12 (Optional) Derivatives of Transcendental Functions
- 3.13 Higher-Order Derivatives
- 3.14 Parting Thoughts
- 4 Applications of Differentiation
- 4.1 Related Rates
- 4.2 Linearization
- 4.3 The Increasing/Decreasing Test
- 4.4 Optimization Theory: Local Extrema
- 4.5 Optimization Theory: Absolute Extrema
- 4.6 Applications of Optimization
- 4.7 What the Second Derivative Tells Us About the Function
- 4.8 Parting Thoughts
- 5 Integration: Adding Up Change
- 5.1 Distance as Area
- 5.2 Leibniz’s Notation for the Integral
- 5.3 The Fundamental Theorem of Calculus
- 5.4 Antiderivatives and the Evaluation Theorem
- 5.5 Indefinite Integrals
- 5.6 Properties of Integrals
- 5.7 Net Signed Area
- 5.8 (Optional) Integrating Transcendental Functions
- 5.9 The Substitution Rule
- 5.10 Applications of Integration
- 5.11 Parting Thoughts
- Epilogue
- Acknowledgments
- Appendix A: Review of Algebra and Geometry
- Appendix B: Review of Functions
- Appendix C: Additional Applied Examples
- Answers to Appendix and Chapter Exercises
- Bibliography
- Index of Applications
- Index of Subjects
"A well-produced and well-written introduction to calculus which nicely balances the technical 'how do you do it' and motivational 'why are we doing this' aspects of the subject."—Nick Lord, Mathematical Gazette
"This reader-friendly book is specifically designed for first-year calculus students. Fernandez writes in a welcoming style and the text is neither repetitive nor jargon-laden. With a strong presentation, well-chosen examples, and useful exercises, he does a marvelous job distilling the subject down to the essentials."—David R. Dorman, Middlebury College
"A brilliant, mind-easing, mind-straightening, and mind-empowering companion guide for all those currently working—and struggling—to discover and understand the meaning and story of calculus."—James Tanton, Mathematical Association of America and Global Math Project
"Calculus Simplified contains just the right amount of content and depth of insight for students who need neither the rigor of a calculus class for mathematicians nor the detail of a calculus class for engineers and physicists. This book balances intuition with theory to present the appropriate level for readers working outside of those subject areas."—John A. Adam, author of A Mathematical Nature Walk
"Calculus Simplified provides an ideal mix of conceptual development of the big ideas and formal treatment of the process. It answers, 'What is calculus?' and 'How do I use it?' without getting bogged down in the muck that often inhibits the joy and productivity for so many students using other materials. This excellent new resource will fill an important niche."—Brent A. Ferguson, Lawrenceville School