If classical Lie groups preserve bilinear vector norms, what Lie groups preserve trilinear, quadrilinear, and higher order invariants? Answering this question from a fresh and original perspective, Predrag Cvitanovic takes the reader on the amazing, four-thousand-diagram journey through the theory of Lie groups. This book is the first to systematically develop, explain, and apply diagrammatic projection operators to construct all semi-simple Lie algebras, both classical and exceptional.
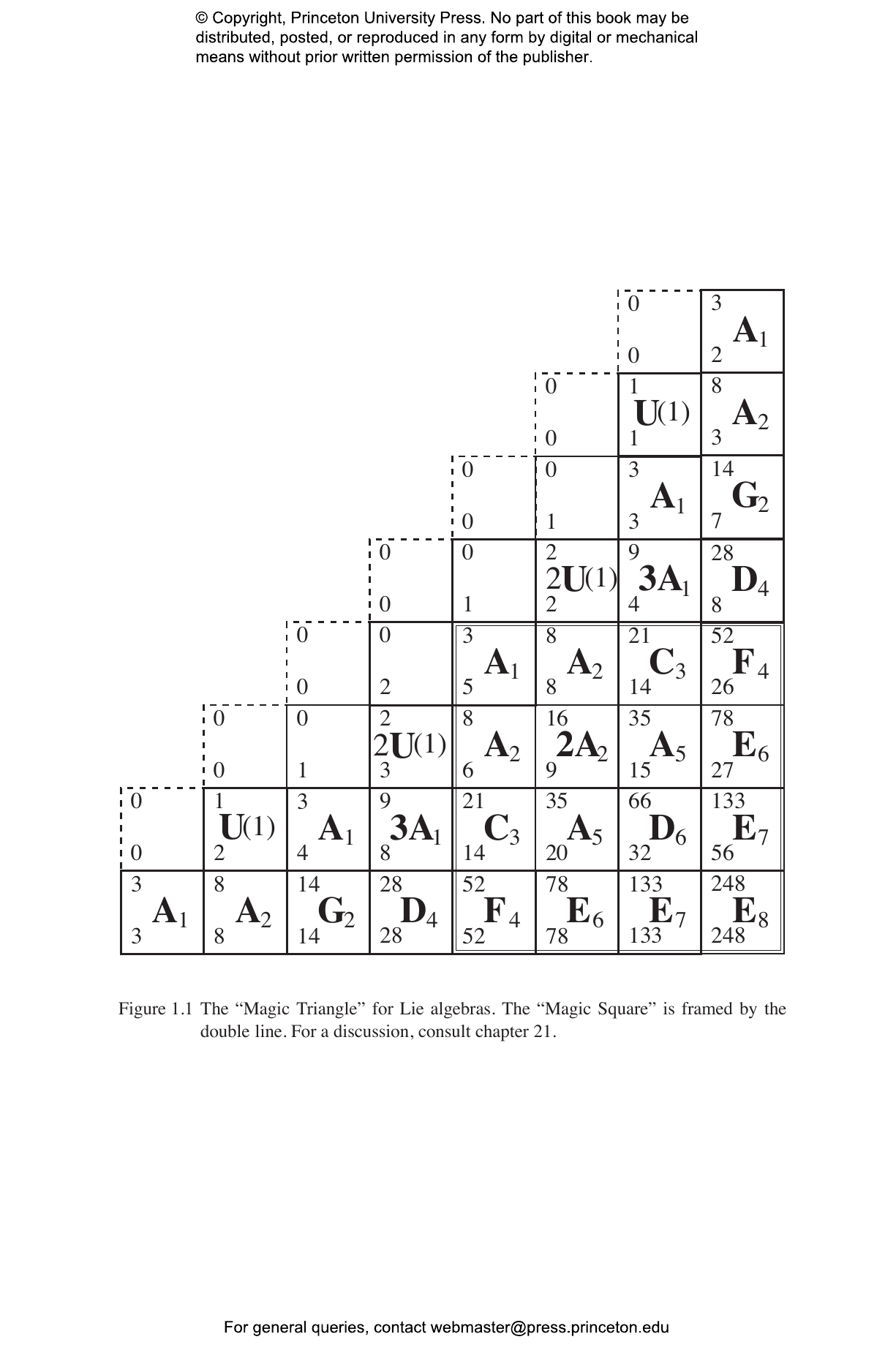
The invariant tensors are presented in a somewhat unconventional, but in recent years widely used, “birdtracks” notation inspired by the Feynman diagrams of quantum field theory. Notably, invariant tensor diagrams replace algebraic reasoning in carrying out all group-theoretic computations. The diagrammatic approach is particularly effective in evaluating complicated coefficients and group weights, and revealing symmetries hidden by conventional algebraic or index notations. The book covers most topics needed in applications from this new perspective: permutations, Young projection operators, spinorial representations, Casimir operators, and Dynkin indices. Beyond this well-traveled territory, more exotic vistas open up, such as “negative dimensional” relations between various groups and their representations. The most intriguing result of classifying primitive invariants is the emergence of all exceptional Lie groups in a single family, and the attendant pattern of exceptional and classical Lie groups, the so-called Magic Triangle. Written in a lively and personable style, the book is aimed at researchers and graduate students in theoretical physics and mathematics.
Predrag Cvitanović is the Glen P. Robinson Professor of Nonlinear Science at the Georgia Institute of Technology. He is the author of Universality in Chaos and lead author of the ChaosBook.org webbook.
"This book has to be seen to be believed! The title, Group Theory, is nothing if not surprising, given that the material dealt with by Predrag Cvitanović in these roughly 250 pages requires a level of sophistication well beyond what is offered in the early stages of university algebra. In point of fact, the general theme of the book under review is Lie theory with representation theory in the foreground, and Cvitanović's revolutionary goal (e.g., 'birdtracks') and, for lack of a better word, the attendant combinatorics. . . . [F]or the right reader, which is to say, an R>0-linear combination of mathematician and physicist equipped with a zeal for novel combinatorics flavored diagram-gymnastics, this book will be a treat and a thrill, and its new and radical way to compute many things Lie is bound to make its mark."—Michael Berg, MAA Reviews
"More than just an innovative notation, this book offers a conceptually novel alternative path to a key mathematical result, the classification of finite-dimensional simple Lie algebras. . . . While this volume is an obvious resource for physics students, the traces of physics that remain in the work will elucidate for mathematics students how physics uses Lie groups as a tool."—D.V. Feldman, Choice
"I think that the book is a very interesting and thought provoking contribution to the literature on representations of compact Lie groups. It has many interesting original aspects that deserve to be known much better than they are."—Karl-Hermann Neeb, Journal of the Lie Theory
"[T]he narrative of the book is written in a relaxed and witty style. The book is intriguing as well as entertaining."—Jeb F. Willenbring, Mathematical Reviews
"In Group Theory, we get a sense of the quest Cvitanović has been on, which makes the book much more fun to read than the average mathematics text. This book is intriguing, novel, and important."—John Baez, University of California, Riverside
"There has been an urgent need for an in-print and readily available version of Cvitanović's innovative and systematic approach to the group-theoretic calculations occurring in theoretical physics and beyond. Well-organized and well-written, this book is definitely an important and valuable contribution to its field."—Alan J. Macfarlane, Cambridge University