Kip Thorne and Roger Blandford’s monumental Modern Classical Physics is now available in five stand-alone volumes that make ideal textbooks for individual graduate or advanced undergraduate courses on statistical physics; optics; elasticity and fluid dynamics; plasma physics; and relativity and cosmology. Each volume teaches the fundamental concepts, emphasizes modern, real-world applications, and gives students a physical and intuitive understanding of the subject.
Statistical Physics is an essential introduction that is different from others on the subject because of its unique approach, which is coordinate-independent and geometric; embraces and elucidates the close quantum-classical connection and the relativistic and Newtonian domains; and demonstrates the power of statistical techniques—particularly statistical mechanics—by presenting applications not only to the usual kinds of things, such as gases, liquids, solids, and magnetic materials, but also to a much wider range of phenomena, including black holes, the universe, information and communication, and signal processing amid noise.
- Includes many exercise problems
- Features color figures, suggestions for further reading, extensive cross-references, and a detailed index
- Optional “Track 2” sections make this an ideal book for a one-quarter, half-semester, or full-semester course
- An online illustration package is available to professors
The five volumes, which are available individually as paperbacks and ebooks, are Statistical Physics; Optics; Elasticity and Fluid Dynamics; Plasma Physics; and Relativity and Cosmology.
Awards and Recognition
- Kip S. Thorne, Co-Winner of the 2017 Nobel Prize in Physics
- Roger D. Blandford, Co-Winner of the 2016 Crafoord Prize in Astronomy and Winner of the 2020 Shaw Prize in Astronomy
Kip S. Thorne, winner of the Nobel Prize in physics, is the Feynman Professor Emeritus of Theoretical Physics at Caltech. His books include Gravitation (Princeton) and Black Holes and Time Warps: Einstein’s Outrageous Legacy. Roger D. Blandford, winner of the Crafoord and Shaw prizes in astronomy, is the Luke Blossom Professor in the School of Humanities and Sciences and founding director of the Kavli Institute for Particle Astrophysics and Cosmology at Stanford University.
- List of Boxes
- Preface
- Contents of Modern Classical Physics, volumes 1–5
- PART I FOUNDATIONS
- 1 Newtonian Physics: Geometric Viewpoint
- 1.1 Introduction
- 1.1.1 The Geometric Viewpoint on the Laws of Physics
- 1.1.2 Purposes of This Chapter
- 1.1.3 Overview of This Chapter
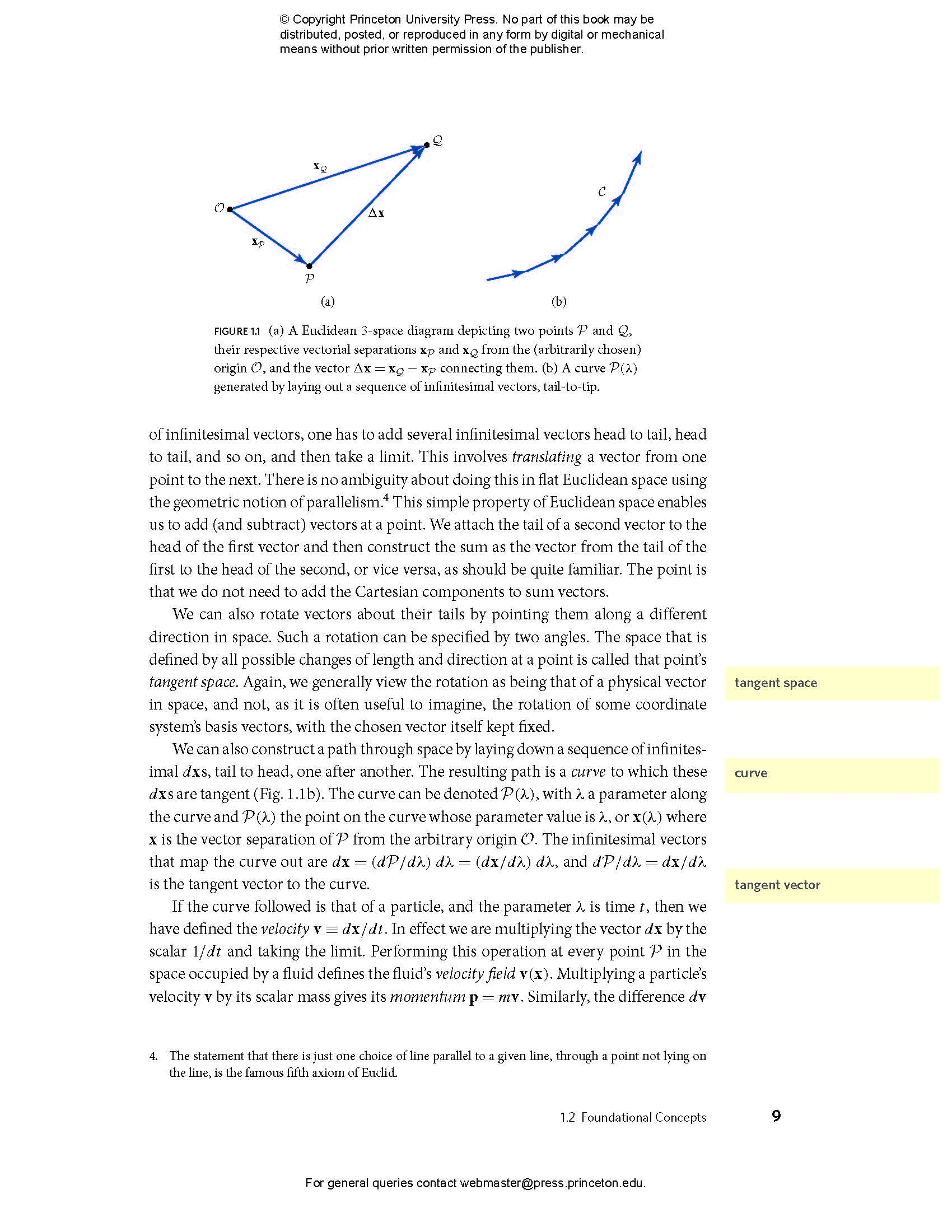
- 1.2 Foundational Concepts
- 1.3 Tensor Algebra without a Coordinate System
- 1.4 Particle Kinetics and Lorentz Force in Geometric Language
- 1.5 Component Representation of Tensor Algebra
- 1.5.1 Slot-Naming Index Notation
- 1.5.2 Particle Kinetics in Index Notation
- 1.6 Orthogonal Transformations of Bases
- 1.7 Differentiation of Scalars, Vectors, and Tensors; Cross Product and Curl
- 1.8 Volumes, Integration, and Integral Conservation Laws
- 1.8.1 Gauss’s and Stokes’ Theorems
- 1.9 The Stress Tensor and Momentum Conservation
- 1.9.1 Examples: Electromagnetic Field and Perfect Fluid
- 1.9.2 Conservation of Momentum
- 1.10 Geometrized Units and Relativistic Particles for Newtonian Readers
- 1.10.1 Geometrized Units
- 1.10.2 Energy and Momentum of a Moving Particle
- Bibliographic Note
- 2 Special Relativity: Geometric Viewpoint
- 2.1 Overview
- 2.2 Foundational Concepts
- 2.2.1 Inertial Frames, Inertial Coordinates, Events, Vectors, and Spacetime Diagrams
- 2.2.2 The Principle of Relativity and Constancy of Light Speed
- 2.2.3 The Interval and Its Invariance
- 2.3 Tensor Algebra without a Coordinate System
- 2.4 Particle Kinetics and Lorentz Force without a Reference Frame
- 2.4.1 Relativistic Particle Kinetics: World Lines, 4-Velocity, 4-Momentum and Its Conservation, 4-Force
- 2.4.2 Geometric Derivation of the Lorentz Force Law
- 2.5 Component Representation of Tensor Algebra
- 2.5.1 Lorentz Coordinates
- 2.5.2 Index Gymnastics
- 2.5.3 Slot-Naming Notation
- 2.6 Particle Kinetics in Index Notation and in a Lorentz Frame
- 2.7 Lorentz Transformations
- 2.8 Spacetime Diagrams for Boosts
- 2.9 Time Travel
- 2.9.1 Measurement of Time; Twins Paradox
- 2.9.2 Wormholes
- 2.9.3 Wormhole as Time Machine
- 2.10 Directional Derivatives, Gradients, and the Levi-Civita Tensor
- 2.11 Nature of Electric and Magnetic Fields; Maxwell’s Equations
- 2.12 Volumes, Integration, and Conservation Laws
- 2.12.1 Spacetime Volumes and Integration
- 2.12.2 Conservation of Charge in Spacetime
- 2.12.3 Conservation of Particles, Baryon Number, and Rest Mass
- 2.13 Stress-Energy Tensor and Conservation of 4-Momentum
- 2.13.1 Stress-Energy Tenso
- 2.13.2 4-Momentum Conservation
- 2.13.3 Stress-Energy Tensors for Perfect Fluids and Electromagnetic Fields
- Bibliographic Note
- PART II STATISTICAL PHYSICS
- 3 Kinetic Theory
- 3.1 Overview
- 3.2 Phase Space and Distribution Function
- 3.2.1 Newtonian Number Density in Phase Space, 𝒩
- 3.2.2 Relativistic Number Density in Phase Space, 𝒩
- 3.2.3 Distribution Function ƒ (x, v, t) for Particles in a Plasma
- 3.2.4 Distribution Function Iⱱ/ⱱ3 for Photons
- 3.2.5 Mean Occupation Number ƞ
- 3.3 Thermal-Equilibrium Distribution Functions
- 3.4 Macroscopic Properties of Matter as Integrals over Momentum Space
- 3.4.1 Particle Density n, Flux S, and Stress Tensor ⊤
- 3.4.2 Relativistic Number-Flux 4-Vector S→ and Stress-Energy Tensor ⊤
- 3.5 Isotropic Distribution Functions and Equations of State
- 3.5.1 Newtonian Density, Pressure, Energy Density, and Equation of State
- 3.5.2 Equations of State for a Nonrelativistic Hydrogen Gas
- 3.5.3 Relativistic Density, Pressure, Energy Density, and Equation of State
- 3.5.4 Equation of State for a Relativistic Degenerate Hydrogen Gas
- 3.5.5 Equation of State for Radiation
- 3.6 Evolution of the Distribution Function: Liouville’s Theorem, the Collisionless Boltzmann Equation, and the Boltzmann Transport Equation
- 3.7 Transport Coefficients
- 3.7.1 Diffusive Heat Conduction inside a Star
- 3.7.2 Order-of-Magnitude Analysis
- 3.7.3 Analysis Using the Boltzmann Transport Equation
- Bibliographic Note
- 4 Statistical Mechanics
- 4.1 Overview
- 4.2 Systems, Ensembles, and Distribution Functions
- 4.2.1 Systems
- 4.2.2 Ensembles
- 4.2.3 Distribution Function
- 4.3 Liouville’s Theorem and the Evolution of the Distribution Function
- 4.4 Statistical Equilibrium
- 4.4.1 Canonical Ensemble and Distribution
- 4.4.2 General Equilibrium Ensemble and Distribution; Gibbs Ensemble Grand Canonical Ensemble
- 4.4.3 Fermi-Dirac and Bose-Einstein Distributions
- 4.4.4 Equipartition Theorem for Quadratic, Classical Degrees of Freedom
- 4.5 The Microcanonical Ensemble
- 4.6 The Ergodic Hypothesis
- 4.7 Entropy and Evolution toward Statistical Equilibrium
- 4.7.1 Entropy and the Second Law of Thermodynamics
- 4.7.2 What Causes the Entropy to Increase?
- 4.8 Entropy per Particle
- 4.9 Bose-Einstein Condensate
- 4.10 Statistical Mechanics in the Presence of Gravity
- 4.10.1 Galaxies
- 4.10.2 Black Holes
- 4.10.3 The Universe
- 4.10.4 Structure Formation in the Expanding Universe: Violent Relaxation and Phase Mixing
- 4.11 Entropy and Information
- 4.11.1 Information Gained When Measuring the State of a System in a Microcanonical Ensemble
- 4.11.2 Information in Communication Theory
- 4.11.3 Examples of Information Content
- 4.11.4 Some Properties of Information
- 4.11.5 Capacity of Communication Channels; Erasing Information from Computer Memories
- Bibliographic Note
- 5 Statistical Thermodynamics
- 5.1 Overview
- 5.2 Microcanonical Ensemble and the Energy Representation of Thermodynamics
- 5.2.1 Extensive and Intensive Variables; Fundamental Potential
- 5.2.2 Energy as a Fundamental Potential
- 5.2.3 Intensive Variables Identified Using Measuring Devices First Law of Thermodynamics
- 5.2.4 Euler’s Equation and Form of the Fundamental Potential
- 5.2.5 Everything Deducible from First Law; Maxwell Relations
- 5.2.6 Representations of Thermodynamics
- 5.3 Grand Canonical Ensemble and the Grand-Potential Representation of Thermodynamics
- 5.3.1 The Grand-Potential Representation, and Computation of Thermodynamic Properties as a Grand Canonical Sum
- 5.3.2 Nonrelativistic van der Waals Gas
- 5.4 Canonical Ensemble and the Physical-Free-Energy Representation of Thermodynamics
- 5.4.1 Experimental Meaning of Physical Free Energy
- 5.4.2 Ideal Gas with Internal Degrees of Freedom
- 5.5 Gibbs Ensemble and Representation of Thermodynamics; Phase Transitions and Chemical Reactions
- 5.5.1 Out-of-Equilibrium Ensembles and Their Fundamental Thermodynamic Potentials and Minimum Principles
- 5.5.2 Phase Transitions
- 5.5.3 Chemical Reactions
- 5.6 Fluctuations away from Statistical Equilibrium
- 5.7 Van der Waals Gas: Volume Fluctuations and Gas-to-Liquid Phase Transition
- 5.8 Magnetic Materials
- 5.8.1 Paramagnetism; The Curie Law
- 5.8.2 Ferromagnetism: The Ising Model
- 5.8.3 Renormalization Group Methods for the Ising Model
- 5.8.4 Monte Carlo Methods for the Ising Model
- Bibliographic Note
- 6 Random Processes
- 6.1 Overview
- 6.2 Fundamental Concepts
- 6.2.1 Random Variables and Random Processes
- 6.2.2 Probability Distributions
- 6.2.3 Ergodic Hypothesis
- 6.3 Markov Processes and Gaussian Processes
- 6.3.1 Markov Processes; Random Walk
- 6.3.2 Gaussian Processes and the Central Limit Theorem; Random Walk
- 6.3.3 Doob’s Theorem for Gaussian-Markov Processes, and Brownian Motion
- 6.4 Correlation Functions and Spectral Densities
- 6.4.1 Correlation Functions; Proof of Doob’s Theorem
- 6.4.2 Spectral Densities
- 6.4.3 Physical Meaning of Spectral Density, Light Spectra, and Noise in a Gravitational Wave Detector
- 6.4.4 The Wiener-Khintchine Theorem; Cosmological Density Fluctuations
- 6.5 2-Dimensional Random Processes
- 6.5.1 Cross Correlation and Correlation Matrix
- 6.5.2 Spectral Densities and the Wiener-Khintchine Theorem
- 6.6 Noise and Its Types of Spectra
- 6.6.1 Shot Noise, Flicker Noise, and Random-Walk Noise; Cesium Atomic Clock
- 6.6.2 Information Missing from Spectral Density
- 6.7 Filtering Random Processes
- 6.7.1 Filters, Their Kernels, and the Filtered Spectral Density
- 6.7.2 Brownian Motion and Random Walks
- 6.7.3 Extracting a Weak Signal from Noise: Band-Pass Filter, Wiener’s Optimal Filter Signal-to-Noise Ratio, and Allan Variance of Clock Noise
- 6.7.4 Shot Noise
- 6.8 Fluctuation-Dissipation Theorem
- 6.8.1 Elementary Version of the Fluctuation-Dissipation Theorem; Langevin Equation Johnson Noise in a Resistor, and Relaxation Time for Brownian Motion
- 6.8.2 Generalized Fluctuation-Dissipation Theorem; Thermal Noise in a Laser Beam’s Measurement of Mirror Motions; Standard Quantum Limit for Measurement Accuracy and How to Evade It
- 6.9 Fokker-Planck Equation
- 6.9.1 Fokker-Planck for a 1-Dimensional Markov Process
- 6.9.2 Optical Molasses: Doppler Cooling of Atoms
- 6.9.3 Fokker-Planck for a Multidimensional Markov Process; Thermal Noise in an Oscillator
- Bibliographic Note
- References
- Name Index
- Subject Index
- Contents of the Unified Work, Modern Classical Physics
- Preface to Modern Classical Physics
- Acknowledgments for Modern Classical Physics
“Extraordinarily impressive.”—Malcolm Longair, Nature
“A magnificent achievement.”—Edward Witten, Physics Today