Kip Thorne and Roger Blandford’s monumental Modern Classical Physics is now available in five stand-alone volumes that make ideal textbooks for individual graduate or advanced undergraduate courses on statistical physics; optics; elasticity and fluid dynamics; plasma physics; and relativity and cosmology. Each volume teaches the fundamental concepts, emphasizes modern, real-world applications, and gives students a physical and intuitive understanding of the subject.
Plasma Physics provides an essential introduction to the subject. A gas that is significantly ionized, usually by heating or photons, a plasma is composed of electrons and ions and sometimes has an embedded or confining magnetic field. Plasmas play a major role in many contemporary applications, phenomena, and fields, including attempts to achieve controlled thermonuclear fusion using magnetic or inertial confinement; in explanations of radio wave propagation in the ionosphere and the behavior of the solar corona and wind; and in astrophysics, where plasmas are responsible for emission throughout the electromagnetic spectrum, including from black holes, highly magnetized neutron stars, and ultrarelativistic outflows. The book also can serve as supplementary reading for many other courses, including in astrophysics, geophysics, and controlled fusion.
- Includes many exercise problems
- Features color figures, suggestions for further reading, extensive cross-references, and a detailed index
- Optional “Track 2” sections make this an ideal book for a one-quarter or one-semester course
- An online illustration package is available to professors
The five volumes, which are available individually as paperbacks and ebooks, are Statistical Physics; Optics; Elasticity and Fluid Dynamics; Plasma Physics; and Relativity and Cosmology.
Awards and Recognition
- Kip S. Thorne, Co-Winner of the 2017 Nobel Prize in Physics
- Roger D. Blandford, Co-Winner of the 2016 Crafoord Prize in Astronomy and Winner of the 2020 Shaw Prize in Astronomy
Kip S. Thorne, winner of the Nobel Prize in physics, is the Feynman Professor Emeritus of Theoretical Physics at Caltech. His books include Gravitation (Princeton) and Black Holes and Time Warps: Einstein’s Outrageous Legacy. Roger D. Blandford, winner of the Crafoord and Shaw prizes in astronomy, is the Luke Blossom Professor in the School of Humanities and Sciences and founding director of the Kavli Institute for Particle Astrophysics and Cosmology at Stanford University.
- List of Boxes
- Preface
- Contents of Modern Classical Physics, volumes 1–5
- 19 Magnetohydrodynamics
- 19.1 Overview
- 19.2 Basic Equations of MHD
- 19.2.1 Maxwell’s Equations in the MHD Approximation
- 19.2.2 Momentum and Energy Conservation
- 19.2.3 Boundary Conditions
- 19.2.4 Magnetic Field and Vorticity
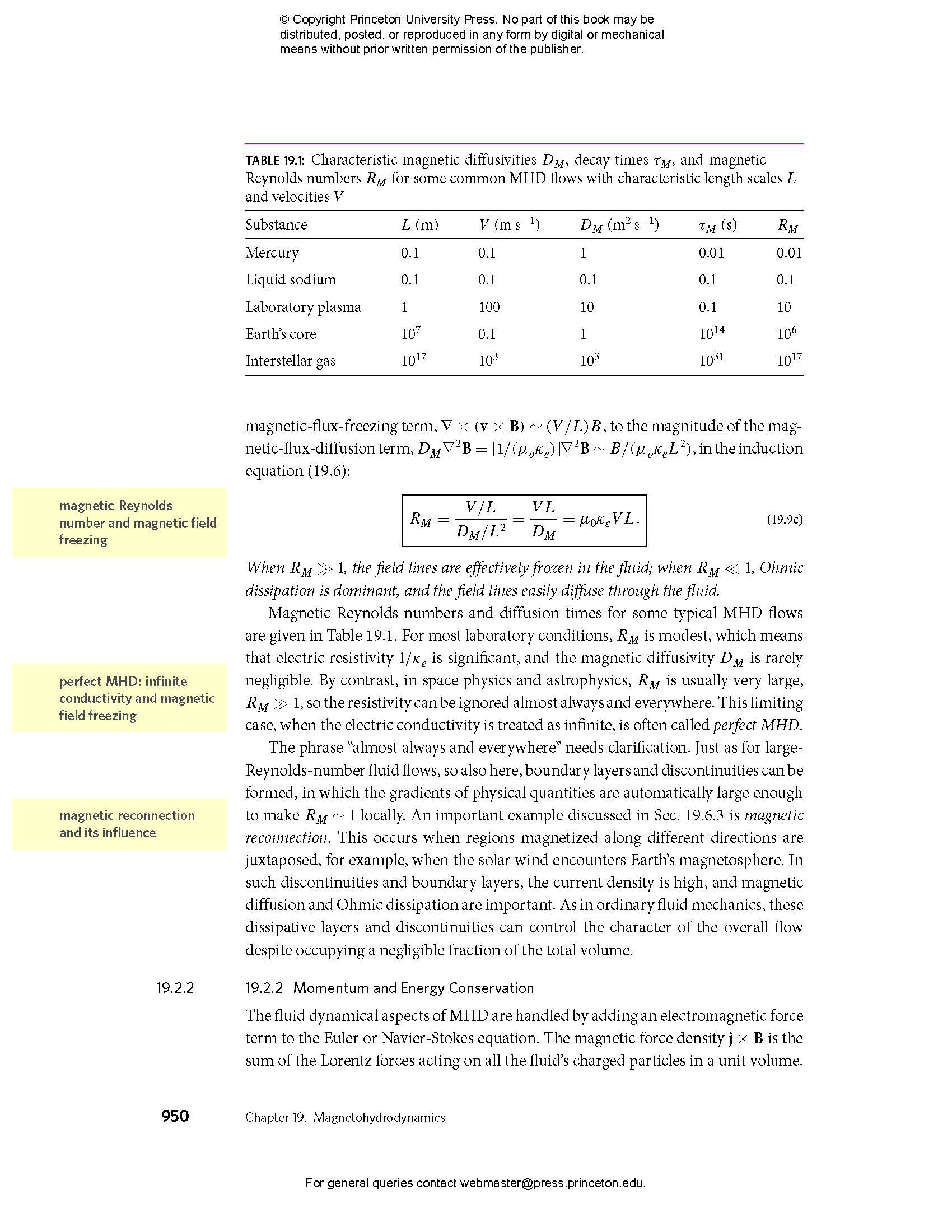
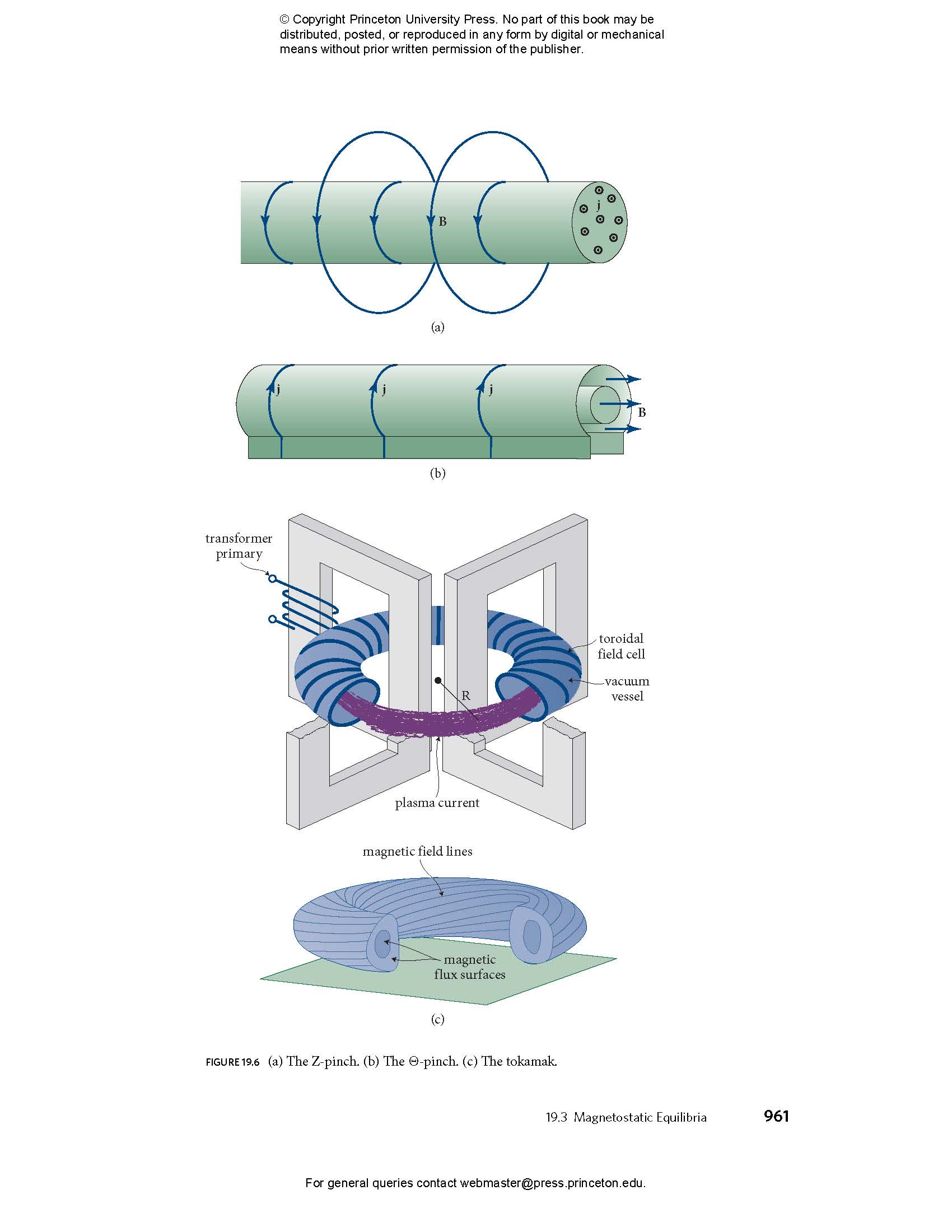
- 19.3 Magnetostatic Equilibria
- 19.3.1 Controlled Thermonuclear Fusion
- 19.3.2 Z-Pinch
- 19.3.3 Θ-Pinch
- 19.3.4 Tokamak
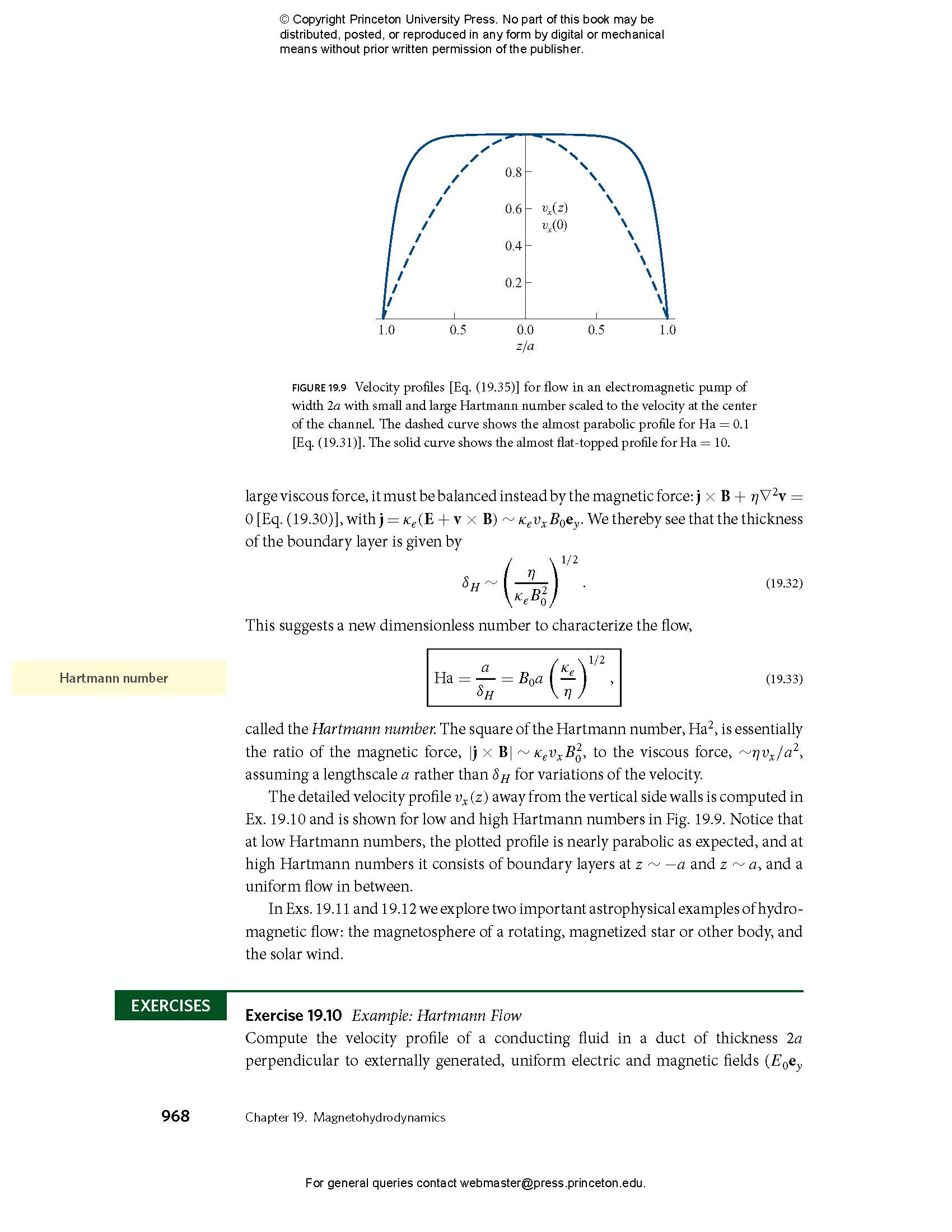
- 19.4 Hydromagnetic Flows
- 19.5 Stability of Magnetostatic Equilibria
- 19.5.1 Linear Perturbation Theory
- 19.5.2 Z-Pinch: Sausage and Kink Instabilities
- 19.5.3 The Θ-Pinch and Its Toroidal Analog; Flute Instability; Motivation for Tokamak
- 19.5.4 Energy Principle and Virial Theorems
- 19.6 Dynamos and Reconnection of Magnetic Field Lines
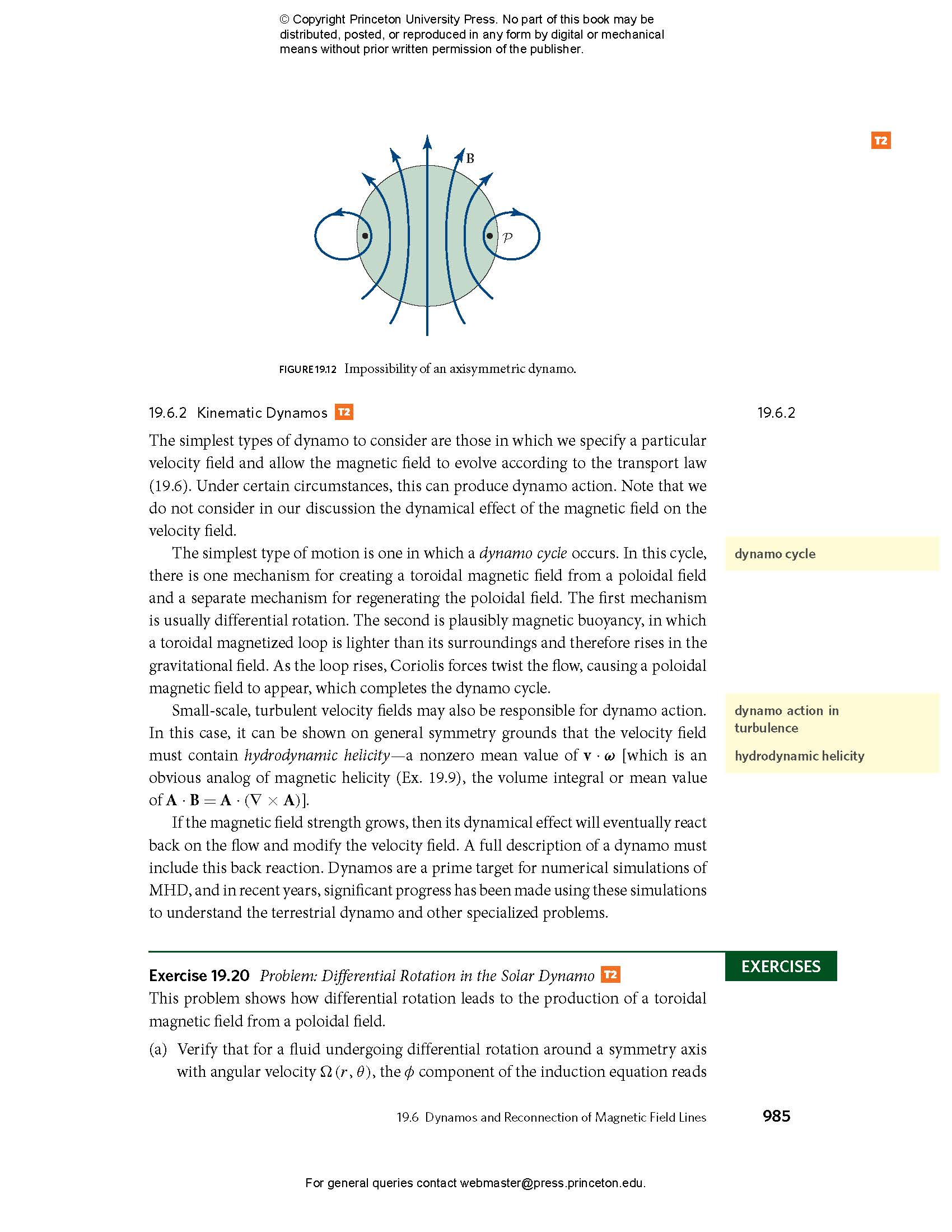
- 19.6.1 Cowling’s Theorem
- 19.6.2 Kinematic Dynamos
- 19.6.3 Magnetic Reconnection
- 19.7 Magnetosonic Waves and the Scattering of Cosmic Rays
- 19.7.1 Cosmic Rays
- 19.7.2 Magnetosonic Dispersion Relation
- 19.7.3 Scattering of Cosmic Rays by Alfvén Waves
- Bibliographic Note
- PART VI PLASMA PHYSICS
- 20 The Particle Kinetics of Plasma
- 20.1 Overview
- 20.2 Examples of Plasmas and Their Density-Temperature Regimes
- 20.2.1 Ionization Boundary
- 20.2.2 Degeneracy Boundary
- 20.2.3 Relativistic Boundary
- 20.2.4 Pair-Production Boundary
- 20.2.5 Examples of Natural and Human-Made Plasmas
- 20.3 Collective Effects in Plasmas—Debye Shielding and Plasma Oscillations
- 20.3.1 Debye Shielding
- 20.3.2 Collective Behavior
- 20.3.3 Plasma Oscillations and Plasma Frequency
- 20.4 Coulomb Collisions
- 20.4.1 Collision Frequency
- 20.4.2 The Coulomb Logarithm
- 20.4.3 Thermal Equilibration Rates in a Plasma
- 20.4.4 Discussion
- 20.5 Transport Coefficients
- 20.5.1 Coulomb Collisions
- 20.5.2 Anomalous Resistivity and Anomalous Equilibration
- 20.6 Magnetic Field
- 20.6.1 Cyclotron Frequency and Larmor Radius
- 20.6.2 Validity of the Fluid Approximation
- 20.6.3 Conductivity Tensor
- 20.7 Particle Motion and Adiabatic Invariants
- 20.7.1 Homogeneous, Time-Independent Magnetic Field and No Electric Field
- 20.7.2 Homogeneous, Time-Independent Electric and Magnetic Fields
- 20.7.3 Inhomogeneous, Time-Independent Magnetic Field
- 20.7.4 A Slowly Time-Varying Magnetic Field
- 20.7.5 Failure of Adiabatic Invariants; Chaotic Orbits
- Bibliographic Note
- 21 Waves in Cold Plasmas: Two-Fluid Formalism
- 21.1 Overview
- 21.2 Dielectric Tensor,Wave Equation, and General Dispersion Relation
- 21.3 Two-Fluid Formalism
- 21.4 Wave Modes in an Unmagnetized Plasma
- 21.4.1 Dielectric Tensor and Dispersion Relation for a Cold, Unmagnetized Plasma
- 21.4.2 Plasma Electromagnetic Modes
- 21.4.3 Langmuir Waves and Ion-Acoustic Waves inWarm Plasmas
- 21.4.4 Cutoffs and Resonances
- 21.5 Wave Modes in a Cold, Magnetized Plasma
- 21.5.1 Dielectric Tensor and Dispersion Relation
- 21.5.2 Parallel Propagation
- 21.5.3 Perpendicular Propagation
- 21.5.4 Propagation of Radio Waves in the Ionosphere; Magnetoionic Theory
- 21.5.5 CMA Diagram forWave Modes in a Cold, Magnetized Plasma
- 21.6 Two-Stream Instability
- Bibliographic Note
- 22 Kinetic Theory ofWarm Plasmas
- 22.1 Overview
- 22.2 Basic Concepts of Kinetic Theory and Its Relationship to Two-Fluid Theory
- 22.2.1 Distribution Function and Vlasov Equation
- 22.2.2 Relation of Kinetic Theory to Two-Fluid Theory
- 22.2.3 Jeans’ Theorem
- 22.3 Electrostatic Waves in an Unmagnetized Plasma: Landau Damping
- 22.3.1 Formal Dispersion Relation
- 22.3.2 Two-Stream Instability
- 22.3.3 The Landau Contour
- 22.3.4 Dispersion Relation forWeakly Damped or Growing Waves
- 22.3.5 Langmuir Waves and Their Landau Damping
- 22.3.6 Ion-Acoustic Waves and Conditions for Their Landau Damping to BeWeak
- 22.4 Stability of Electrostatic Waves in Unmagnetized Plasmas
- 22.4.1 Nyquist’s Method
- 22.4.2 Penrose’s Instability Criterion
- 22.5 Particle Trapping
- 22.6 𝒩-Particle Distribution Function
- 22.6.1 BBGKY Hierarchy
- 22.6.2 Two-Point Correlation Function
- 22.6.3 Coulomb Correction to Plasma Pressure
- Bibliographic Note
- 23 Nonlinear Dynamics of Plasmas
- 23.1 Overview
- 23.2 Quasilinear Theory in Classical Language
- 23.2.1 Classical Derivation of the Theory
- 23.2.2 Summary of Quasilinear Theory
- 23.2.3 Conservation Laws
- 23.2.4 Generalization to 3 Dimensions
- 23.3 Quasilinear Theory in Quantum Mechanical Language
- 23.3.1 Plasmon Occupation Number 𝜂
- 23.3.2 Evolution of 𝜂 for Plasmons via Interaction with Electrons
- 23.3.3 Evolution of 𝑓 for Electrons via Interaction with Plasmons
- 23.3.4 Emission of Plasmons by Particles in the Presence of a Magnetic Field
- 23.3.5 Relationship between Classical and Quantum Mechanical Formalisms
- 23.3.6 Evolution of 𝜂 via Three-Wave Mixing
- 23.4 Quasilinear Evolution of Unstable Distribution Functions—A Bump in the Tail
- 23.4.1 Instability of Streaming Cosmic Rays
- 23.5 Parametric Instabilities; Laser Fusion
- 23.6 Solitons and Collisionless Shock Waves
- Bibliographic Note
- App. A Evolution of Vorticity
- 14.2 Vorticity, Circulation, and Their Evolution
- 14.2.1 Vorticity Evolution
- 14.2.2 Barotropic, Inviscid, Compressible Flows: Vortex Lines Frozen into Fluid
- App. B Geometric Optics
- 7.2 Waves in a Homogeneous Medium
- 7.2.1 Monochromatic Plane Waves; Dispersion Relation
- 7.2.2 Wave Packets
- 7.3 Waves in an Inhomogeneous, Time-Varying Medium: The Eikonal Approximation and Geometric Optics
- 7.3.1 Geometric Optics for a Prototypical Wave Equation
- 7.3.2 Connection of Geometric Optics to Quantum Theory
- 7.3.3 Geometric Optics for a General Wave
- 7.3.4 Examples of Geometric-Optics Wave Propagation
- 7.3.5 Relation to Wave Packets; Limitations of the Eikonal Approximation and Geometric Optics
- 7.3.6 Fermat’s Principle
- App. C Distribution Function and Mean Occupation Number
- 3.2 Phase Space and Distribution Function
- 3.2.1 Newtonian Number Density in Phase Space, 𝒩
- 3.2.3 Distribution Function f (x, v, t) for Particles in a Plasma
- 3.2.5 Mean Occupation Number 𝜂
- References
- Name Index
- Subject Index
- Contents of the Unified Work, Modern Classical Physics
- Preface to Modern Classical Physics
- Acknowledgments for Modern Classical Physics
“Extraordinarily impressive.”—Malcolm Longair, Nature
“A magnificent achievement.”—Edward Witten, Physics Today