Of all the academic disciplines, mathematics is perhaps the most difficult to popularize. One must navigate a subject that is not always received with excitement by the general public. Worse still, mathematics uses highly specialized language that employs a peculiar jargon and a multitude of symbols. If we are to advocate for this discipline and give it the wide coverage it deserves, we must address these challenges and meet them head on. One way to do this is for mathematically-versed authors to write books that describe their work with language and images that the layperson can relate to but without compromising the accuracy of the subject matter. It is also important to give our discipline a human face by bringing to life the individuals whose names adorn countless equations and theorems across the mathematical profession.
Even within the many subdivisions of modern mathematics, some areas lend themselves easier to popularization than others. Geometry immediately comes to mind. Here we can form a visual image of a particular statement, be it an abstract theorem or a relationship between points, lines, or circles. Take, for example, the equation a2 + b2 = c2. Most people will immediately recognize it as the Pythagorean Theorem: in a right triangle, the square built on the hypotenuse equals in area to the combined area of the squares built on the two other sides (see figure 1 by Eugen Jost). In fact, this famous geometric configuration has once been proposed as a means of communication with the putative inhabitants of the Moon. The idea was to plant somewhere in the steppes of Siberia a huge field shaped in the form of a right triangle with its attendant squares. Our lunarian neighbors would surely recognize the universal meaning of this shape and respond in kind. The origin of this idea is attributed to none other than the great mathematician Carl Friedrich Gauss (1777–1855).

It was this goal of popularizing geometry that guided Eugen Jost and me in writing our first collaborative book, Beautiful Geometry. We decided to cover a wide range of geometric themes in roughly chronological order, beginning with Thales of Miletus (sixth century BCE) and leading up to our own time. Our collaboration began in 2007 when we met in the small town of Aarau, Switzerland, where I was asked to give a talk to the senior class of their cantonal high school. This school has a claim of fame: young Albert Einstein spent two years here when he was 16 or 17 years old. The school’s main building hasn’t changed since those years in the late nineteenth century. My talk was titled “Mysteries of Infinity,” and among the attendants was Eugen—who was already known to me as an artist of exquisitely beautiful works based on number patterns and geometric shapes, all exhibited in dazzling colors. After my talk, we met for lunch and immediately bonded. Beautiful Geometry was born that day.
In our second collaborative book, Pentagons and Pentagrams: an Illustrated History, we decided to focus on a single shape, the pentagon with its associated pentagram (a five-pointed star polygon). This peculiar shape has a rich history going back to the Pythagoreans, who regarded it as a symbol of friendship and brotherhood. It has also acquired a spiritual significance, especially in the Mediterranean and Middle East regions, and it played a role in architecture, from the Medieval five-sided fortresses to the Pentagon in Washington, D.C. All this is intertwined with the pentagon’s many mathematical features, including its close relation to the golden ratio.
In our own time, the pentagon has assumed an entirely new role with the unexpected discovery of fivefold symmetries in a hitherto unknown type of alloy known as quasicrystal. This discovery embroiled its discoverer—Professor Dan Shechtman of the Technion, Israel’s flagship technological institute—in a bitter controversy, as it ran contrary to all accepted notions of how crystals should form. In the end, Shechtman was completely vindicated, and his discovery earned him the Nobel Prize in Chemistry. The story of this landmark event has all the elements of a human drama in which theoretical and experimental science, personal prejudices, and ultimate triumph are interlaced in a thrilling saga.
But it isn’t only geometric shapes that can leave a strong visual impression on the viewer; sometimes an equation can do the same, catching our attention for its sheer simplicity and elegance. Such is the case with Binet’s formula, named after Jacques Philippe Marie Binet (1786-1856), a French mathematician who specialized in number theory and algebra:
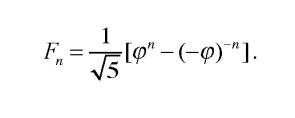
Here Fn denotes the nth Fibonacci number and φ is the golden ratio, an irrational number approximately equal to 1.618 (its exact value is (1+√5)/2 ). Binet found the formula in 1843, but it was already known to Abraham de Moivre, Daniel Bernoulli, and Leonhard Euler a century earlier. Justly or not, the name stuck.
Binet’s formula is remarkable because it combines two concepts from seemingly unrelated branches of mathematics: number theory and geometry. The Fibonacci sequence starts with 1 and again 1, with each subsequent member being the sum of its two predecessors: 1, 1, 2, 3, 5, 8, 13, 21, 34, …. Italian mathematician Leonardo Fibonacci (ca.1170-1250) popularized it in his book Liber abaci (“Book of the Calculation”), published in Pisa in 1202. The sequence arose in connection with a recreational problem that he posed as a riddle in his book: a pair of rabbits produces an offspring at the end of their first month and every month thereafter. The offspring then repeat the same schedule. How many rabbits will there be at the end of the first year? It is easy to see that the number of rabbits follows the Fibonacci sequence, whose twelfth member is 144 (see figure 2 by Eugen Jost).

The other element in Binet’s formula is the golden ratio. It was first discussed by the Pythagoreans, who realized that it is the key to constructing the regular pentagon with Euclidean tools (a straightedge and a compass). That discovery would acquire something of a mythical aura over the coming centuries for its alleged role in the theory of proportions. A rectangle with length-to-width ratio equal to φ has been claimed to have an especially pleasing proportion, and quite a few artists have based their designs on this particular ratio. Whether true or false, the aura surrounding the golden ratio persists to this day (see figure 3 by Eugen Jost).

Once upon a time, writing popular science books was not looked favorably upon in academic circles, but that has changed in the past two or three decades. University publishing houses have released many excellent popular books on a wide range of topics, and the list is still growing. Princeton University Press has included dozens of popular works on all aspects of mathematics as part of its Princeton Science Library of classic works of lasting value. It is safe to say that the views on popularizing science have changed for good.
Eli Maor is a former professor of the history of mathematics at Loyola University Chicago. His books include the internationally acclaimed To Infinity and Beyond, e: The Story of a Number, The Pythagorean Theorem: A 4,000-Year History, Music by the Numbers, and with Eugen Jost, Beautiful Geometry (all Princeton). Eugen Jost is a well-known Swiss artist whose work is strongly influenced by mathematics.

