Kip Thorne and Roger Blandford’s monumental Modern Classical Physics is now available in five stand-alone volumes that make ideal textbooks for individual graduate or advanced undergraduate courses on statistical physics; optics; elasticity and fluid dynamics; plasma physics; and relativity and cosmology. Each volume teaches the fundamental concepts, emphasizes modern, real-world applications, and gives students a physical and intuitive understanding of the subject.
Elasticity and Fluid Dynamics provides an essential introduction to these subjects. Fluids and elastic solids are everywhere—from Earth’s crust and skyscrapers to ocean currents and airplanes. They are central to modern physics, astrophysics, the Earth sciences, biophysics, medicine, chemistry, engineering, and technology, and this centrality has intensified in recent years—so much so that a basic understanding of the behavior of elastic solids and fluids should be part of the repertoire of every physicist and engineer and almost every other natural scientist. While both elasticity and fluid dynamics involve continuum physics and use similar mathematical tools and modes of reasoning, each subject can be readily understood without the other, and the book allows them to be taught independently, with the first two chapters introducing and covering elasticity and the last six doing the same for fluid dynamics. The book also can serve as supplementary reading for many other courses, including in astrophysics, geophysics, and aerodynamics.
- Includes many exercise problems
- Features color figures, suggestions for further reading, extensive cross-references, and a detailed index
- Optional “Track 2” sections make this an ideal book for a one-quarter or one-semester course in elasticity, fluid dynamics, or continuum physics
- An online illustration package is available to professors
The five volumes, which are available individually as paperbacks and ebooks, are Statistical Physics; Optics; Elasticity and Fluid Dynamics; Plasma Physics; and Relativity and Cosmology.
Awards and Recognition
- Kip S. Thorne, Co-Winner of the 2017 Nobel Prize in Physics
- Roger D. Blandford, Co-Winner of the 2016 Crafoord Prize in Astronomy and Winner of the 2020 Shaw Prize in Astronomy
Kip S. Thorne, winner of the Nobel Prize in physics, is the Feynman Professor Emeritus of Theoretical Physics at Caltech. His books include Gravitation (Princeton) and Black Holes and Time Warps: Einstein’s Outrageous Legacy. Roger D. Blandford, winner of the Crafoord and Shaw prizes in astronomy, is the Luke Blossom Professor in the School of Humanities and Sciences and founding director of the Kavli Institute for Particle Astrophysics and Cosmology at Stanford University.
- List of Boxes
- Preface
- Contents of Modern Classical Physics, volumes 1–5
- PART IV ELASTICITY
- 11 Elastostatics
- 11.1 Overview
- 11.2 Displacement and Strain
- 11.2.1 Displacement Vector and Its Gradient
- 11.2.2 Expansion, Rotation, Shear, and Strain
- 11.3 Stress, Elastic Moduli, and Elastostatic Equilibrium
- 11.3.1 Stress Tensor
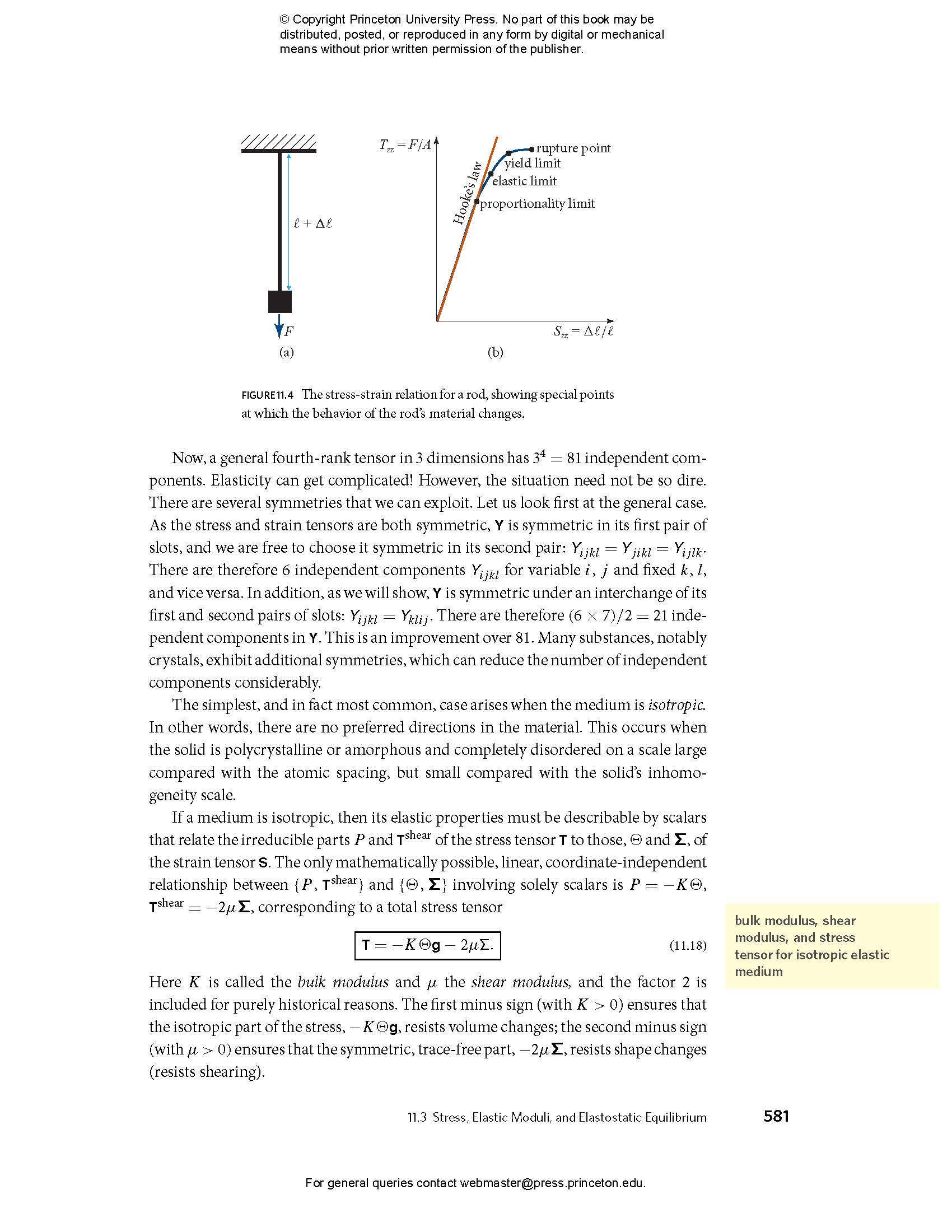
- 11.3.2 Realm of Validity for Hooke’s Law
- 11.3.3 Elastic Moduli and Elastostatic Stress Tensor
- 11.3.4 Energy of Deformation
- 11.3.5 Thermoelasticity
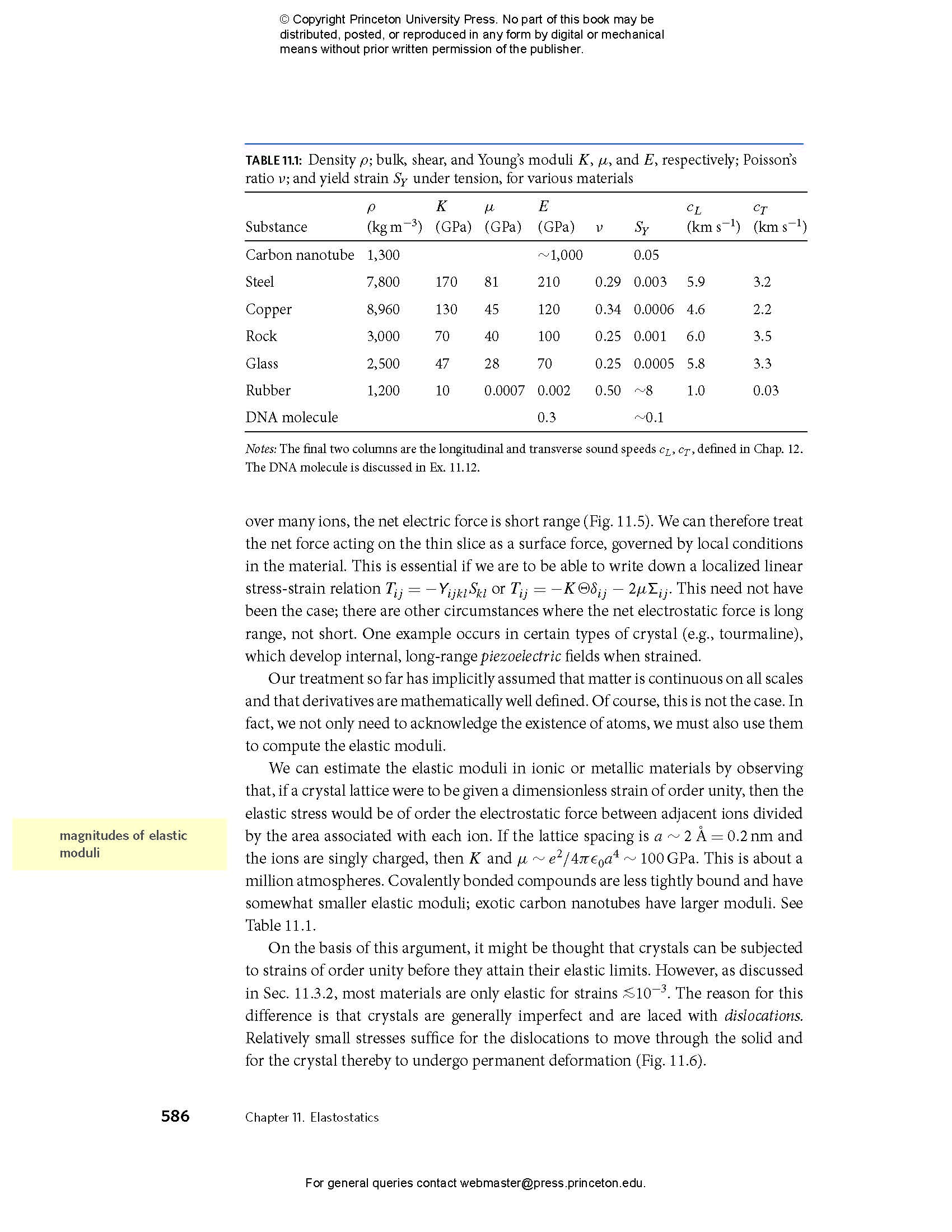
- 11.3.6 Molecular Origin of Elastic Stress; Estimate of Moduli
- 11.3.7 Elastostatic Equilibrium: Navier-Cauchy Equation
- 11.4 Young’s Modulus and Poisson’s Ratio for an Isotropic Material: A Simple Elastostatics Problem
- 11.5 Reducing the Elastostatic Equations to 1 Dimension for a Bent Beam: Cantilever Bridge, Foucault Pendulum, DNA Molecule, Elastica
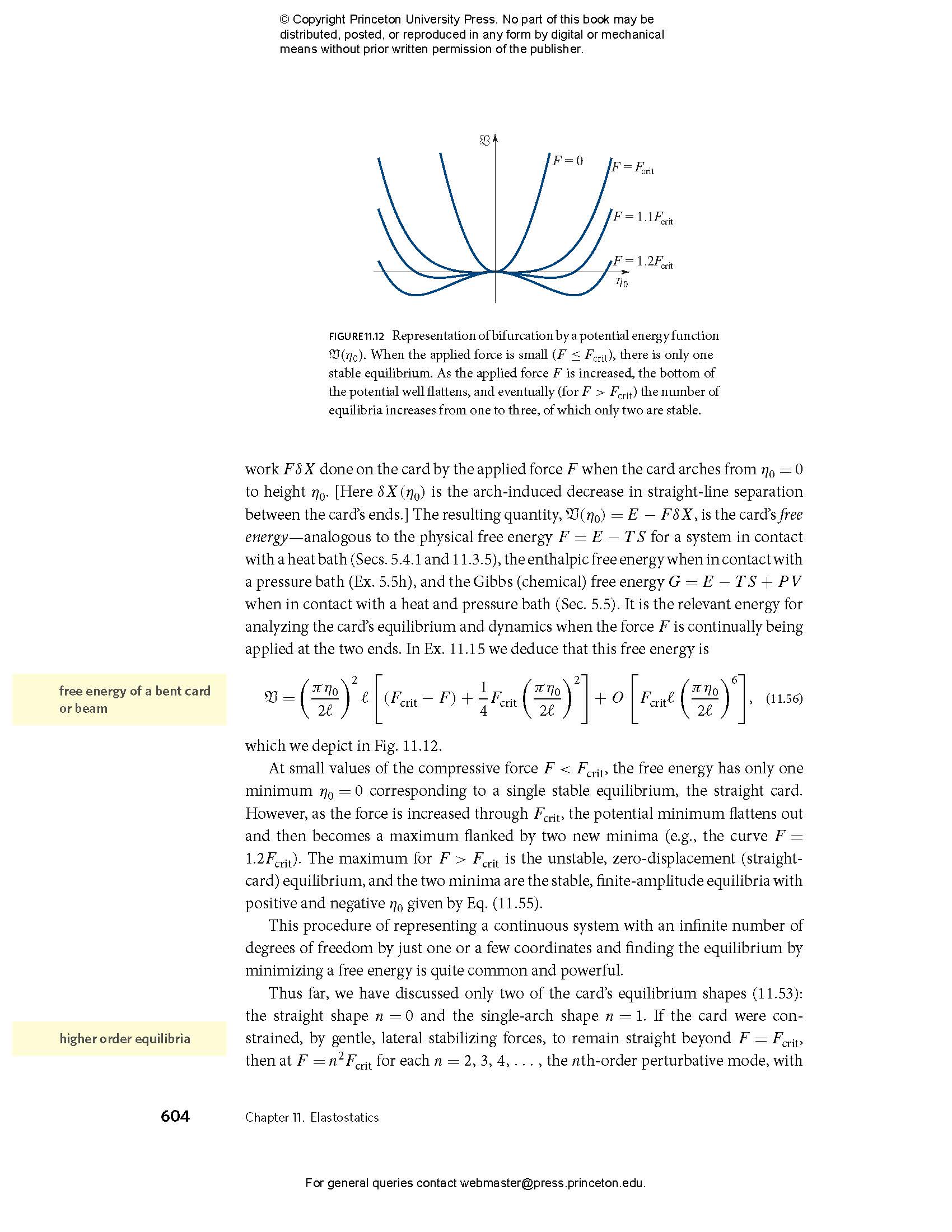
- 11.6 Buckling and Bifurcation of Equilibria
- 11.6.1 Elementary Theory of Buckling and Bifurcation
- 11.6.2 Collapse of theWorld Trade Center Buildings
- 11.6.3 Buckling with Lateral Force; Connection to Catastrophe Theory
- 11.6.4 Other Bifurcations: Venus Fly Trap, Whirling Shaft, Triaxial Stars, and Onset of Turbulence
- 11.7 Reducing the Elastostatic Equations to 2 Dimensions for a Deformed Thin Plate: Stress Polishing a Telescope Mirror
- 11.8 Cylindrical and Spherical Coordinates: Connection Coefficients and Components of the Gradient of the Displacement Vector
- 11.9 Solving the 3-Dimensional Navier-Cauchy Equation in Cylindrical Coordinates
- 11.9.1 Simple Methods: Pipe Fracture and Torsion Pendulum
- 11.9.2 Separation of Variables and Green’s Functions: Thermoelastic Noise in Mirrors
- Bibliographic Note
- 12 Elastodynamics
- 12.1 Overview
- 12.2 Basic Equations of Elastodynamics; Waves in a Homogeneous Medium
- 12.2.1 Equation of Motion for a Strained Elastic Medium
- 12.2.2 Elastodynamic Waves
- 12.2.3 Longitudinal Sound Waves
- 12.2.4 Transverse Shear Waves
- 12.2.5 Energy of Elastodynamic Waves
- 12.3 Waves in Rods, Strings, and Beams
- 12.3.1 Compression Waves in a Rod
- 12.3.2 Torsion Waves in a Rod
- 12.3.3 Waves on Strings
- 12.3.4 Flexural Waves on a Beam
- 12.3.5 Bifurcation of Equilibria and Buckling (Once More)
- 12.4 Body Waves and Surface Waves—Seismology and Ultrasound
- 12.4.1 Body Waves
- 12.4.2 Edge Waves
- 12.4.3 Green’s Function for a Homogeneous Half-Space
- 12.4.4 Free Oscillations of Solid Bodies
- 12.4.5 Seismic Tomography
- 12.4.6 Ultrasound; Shock Waves in Solids
- 12.5 The Relationship of Classical Waves to Quantum Mechanical Excitations
- Bibliographic Note
- PART V FLUID DYNAMICS
- 13 Foundations of Fluid Dynamic
- 13.1 Overview
- 13.2 The Macroscopic Nature of a Fluid: Density, Pressure, Flow Velocity; Liquids versus Gases
- 13.3 Hydrostatics
- 13.3.1 Archimedes’ Law
- 13.3.2 Nonrotating Stars and Planets
- 13.3.3 Rotating Fluids
- 13.4 Conservation Laws
- 13.5 The Dynamics of an Ideal Fluid
- 13.5.1 Mass Conservation
- 13.5.2 Momentum Conservation
- 13.5.3 Euler Equation
- 13.5.4 Bernoulli’s Theorem
- 13.5.5 Conservation of Energy
- 13.6 Incompressible Flows
- 13.7 Viscous Flows with Heat Conduction
- 13.7.1 Decomposition of the Velocity Gradient into Expansion, Vorticity, and Shear
- 13.7.2 Navier-Stokes Equation
- 13.7.3 Molecular Origin of Viscosity
- 13.7.4 Energy Conservation and Entropy Production
- 13.7.5 Reynolds Number
- 13.7.6 Pipe Flow
- 13.8 Relativistic Dynamics of a Perfect Fluid
- 13.8.1 Stress-Energy Tensor and Equations of Relativistic Fluid Mechanics
- 13.8.2 Relativistic Bernoulli Equation and Ultrarelativistic Astrophysical Jets
- 13.8.3 Nonrelativistic Limit of the Stress-Energy Tensor
- Bibliographic Note
- 14 Vorticity
- 14.1 Overview
- 14.2 Vorticity, Circulation, and Their Evolution
- 14.3 Low-Reynolds-Number Flow—Stokes Flow and Sedimentation
- 14.3.1 Motivation: Climate Change
- 14.3.2 Stokes Flow
- 14.3.3 Sedimentation Rate
- 14.4 High-Reynolds-Number Flow—Laminar Boundary Layers
- 14.4.1 Blasius Velocity Profile Near a Flat Plate: Stream Function and Similarity Solution
- 14.4.2 Blasius Vorticity Profile
- 14.4.3 Viscous Drag Force on a Flat Plate
- 14.4.4 Boundary Layer Near a Curved Surface: Separation
- 14.5 Nearly Rigidly Rotating Flows—Earth’s Atmosphere and Oceans
- 14.5.1 Equations of Fluid Dynamics in a Rotating Reference Frame
- 14.5.2 Geostrophic Flows
- 14.5.3 Taylor-Proudman Theorem
- 14.5.4 Ekman Boundary Layers
- 14..6 Instabilities of Shear Flows—Billow Clouds and Turbulence in the Stratosphere
- 14.6.1 Discontinuous Flow: Kelvin-Helmholtz Instability
- 14.6.2 Discontinuous Flow with Gravity
- 14.6.3 Smoothly Stratified Flows: Rayleigh and Richardson Criteria for Instability
- Bibliographic Note
- 15 Turbulence
- 15.1 Overview
- 15.2 The Transition to Turbulence—Flow Past a Cylinder
- 15.3 Empirical Description of Turbulence
- 15.4 Semiquantitative Analysis of Turbulence
- 15.4.1 Weak-Turbulence Formalism
- 15.4.2 Turbulent Viscosity
- 15.4.3 TurbulentWakes and Jets; Entrainment; the Coanda Effect
- 15.4.4 Kolmogorov Spectrum for Fully Developed, Homogeneous, Isotropic Turbulence
- 15.5 Turbulent Boundary Layers
- 15.5.1 Profile of a Turbulent Boundary Layer
- 15.5.2 Coanda Effect and Separation in a Turbulent Boundary Layer
- 15.5.3 Instability of a Laminar Boundary Layer
- 15.5.4 Flight of a Ball
- 15.6 The Route to Turbulence—Onset of Chaos
- 15.6.1 Rotating Couette Flow
- 15.6.2 Feigenbaum Sequence, Poincaré Maps, and the Period-Doubling Route to Turbulence in Convection
- 15.6.3 Other Routes to Turbulent Convection
- 15.6.4 Extreme Sensitivity to Initial Conditions
- Bibliographic Note
- 16 Waves
- 16.1 Overview
- 16.2 Gravity Waves on and beneath the Surface of a Fluid
- 16.2.1 Deep-Water Waves and Their Excitation and Damping
- 16.2.2 Shallow-Water Waves
- 16.2.3 Capillary Waves and Surface Tension
- 16.2.4 Helioseismology
- 16.3 Nonlinear Shallow-Water Waves and Solitons
- 16.3.1 Korteweg–de Vries (KdV) Equation
- 16.3.2 Physical Effects in the KdV Equation
- 16.3.3 Single-Soliton Solution
- 16.3.4 Two-Soliton Solution
- 16.3.5 Solitons in Contemporary Physics
- 16.4 Rossby Waves in a Rotating Fluid
- 16.5 Sound Waves
- 16.5.1 Wave Energy
- 16.5.2 Sound Generation
- 16.5.3 Radiation Reaction, Runaway Solutions, and Matched Asymptotic Expansions
- Bibliographic Note
- 17 Compressible and Supersonic Flow
- 17.1 Overview
- 17.2 Equations of Compressible Flow
- 17.3 Stationary, Irrotational, Quasi-1-Dimensional Flow
- 17.3.1 Basic Equations; Transition from Subsonic to Supersonic Flow
- 17.3.2 Setting up a Stationary, Transonic Flow
- 17.3.3 Rocket Engines
- 17.4 Dimensional, Time-Dependent Flow
- 17.4.1 Riemann Invariants
- 17.4.2 Shock Tube
- 17.5 Shock Fronts
- 17.5.1 Junction Conditions across a Shock; Rankine-Hugoniot Relations
- 17.5.2 Junction Conditions for Ideal Gas with Constant γ
- 17.5.3 Internal Structure of a Shock
- 17.5.4 Mach Cone
- 17.6 Self-Similar Solutions—Sedov-Taylor BlastWave
- 17.6.1 The Sedov-Taylor Solution
- 17.6.2 Atomic Bomb
- 17.6.3 Supernovae
- Bibliographic Note
18 Convection- 18.1 Overview
- 18.2 Diffusive Heat Conduction—Cooling a Nuclear Reactor; Thermal Boundary Layers
- 18.3 Boussinesq Approximation
- 18.4 Rayleigh-Bénard Convection
- 18.5 Convection in Stars
- 18.6 Double Diffusion—Salt Fingers
- Bibliographic Note
App. A Newtonian Physics: Geometric Viewpoint- 1.1 Introduction
- 1.1.1 The Geometric Viewpoint on the Laws of Physics
- 1.1.2 Purposes of This Chapter
- 1.1.3 Overview of This Chapter
- 1.2 Foundational Concepts
- 1.3 Tensor Algebra without a Coordinate System
- 1.4 Particle Kinetics and Lorentz Force in Geometric Language
- 1.5 Component Representation of Tensor Algebra
- 1.5.1 Slot-Naming Index Notation
- 1.5.2 Particle Kinetics in Index Notation
- 1.6 Orthogonal Transformations of Bases
- 1.7 Differentiation of Scalars, Vectors, and Tensors; Cross Product and Curl
- 1.8 Volumes, Integration, and Integral Conservation Laws
- 1.8.1 Gauss’s and Stokes’ Theorems
- 11.9 The Stress Tensor and Momentum Conservation
- 1.9.1 Examples: Electromagnetic Field and Perfect Fluid
- 1.9.2 Conservation of Momentum
- 1.10 Geometrized Units and Relativistic Particles for Newtonian Readers
- 1.10.1 Geometrized Units
- 1.10.2 Energy and Momentum of a Moving Particle
- Bibliographic Note
ReferencesName IndexContents of the Unified Work, Modern Classical PhysicsPreface to Modern Classical PhysicsAcknowledgments for Modern Classical Physics
“Extraordinarily impressive.”—Malcolm Longair, Nature
“A magnificent achievement.”—Edward Witten, Physics Today