Modern Classical Physics: Optics, Fluids, Plasmas, Elasticity, Relativity, and Statistical Physics
A groundbreaking text and reference book on twenty-first-century classical physics and its applications


Hardcover
- Price:
- $150.00/£125.00
- ISBN:
- Published:
- Sep 5, 2017
- Copyright:
- 2018
- Pages:
- 1552
- Size:
- 8 x 10 in.
- Illus:
- 349 color illus. 6 halftones. 15 tables.
- Main_subject:
- Physics & Astronomy
ebook
- Price:
- $150.00/£125.00
- ISBN:
- Published:
- Sep 5, 2017
- Copyright:
- 2018
- Pages:
- 1552
- Size:
- 8 x 10 in.
- Illus:
- 349 color illus. 6 halftones. 15 tables.
- Main_subject:
- Physics & Astronomy
This first-year graduate-level text and reference book covers the fundamental concepts and twenty-first-century applications of six major areas of classical physics that every masters- or PhD-level physicist should be exposed to, but often isn’t: statistical physics, optics (waves of all sorts), elastodynamics, fluid mechanics, plasma physics, and special and general relativity and cosmology. Growing out of a full-year course that the eminent researchers Kip Thorne and Roger Blandford taught at Caltech for almost three decades, this book is designed to broaden the training of physicists. Its six main topical sections are also designed so they can be used in separate courses, and the book provides an invaluable reference for researchers.
- Presents all the major fields of classical physics except three prerequisites: classical mechanics, electromagnetism, and elementary thermodynamics
- Elucidates the interconnections between diverse fields and explains their shared concepts and tools
- Focuses on fundamental concepts and modern, real-world applications
- Takes applications from fundamental, experimental, and applied physics; astrophysics and cosmology; geophysics, oceanography, and meteorology; biophysics and chemical physics; engineering and optical science and technology; and information science and technology
- Emphasizes the quantum roots of classical physics and how to use quantum techniques to elucidate classical concepts or simplify classical calculations
- Features hundreds of color figures, some five hundred exercises, extensive cross-references, and a detailed index
- An online illustration package is available
Awards and Recognition
- Winner of the 2018 PROSE Award in Textbook / Physical Sciences and Mathematics, Association of American Publishers
- Kip S. Thorne, Co-Winner of the 2017 Nobel Prize in Physics
- Roger D. Blandford, Co-Winner of the 2016 Crafoord Prize in Astronomy and Winner of the 2020 Shaw Prize in Astronomy
- List of Boxes
- Preface
- Acknowledgments
- PART I FOUNDATIONS
- 1 Newtonian Physics: Geometric Viewpoint
- 1.1 Introduction
- 1.1.1 The Geometric Viewpoint on the Laws of Physics
- 1.1.2 Purposes of This Chapter
- 1.1.3 Overview of This Chapter
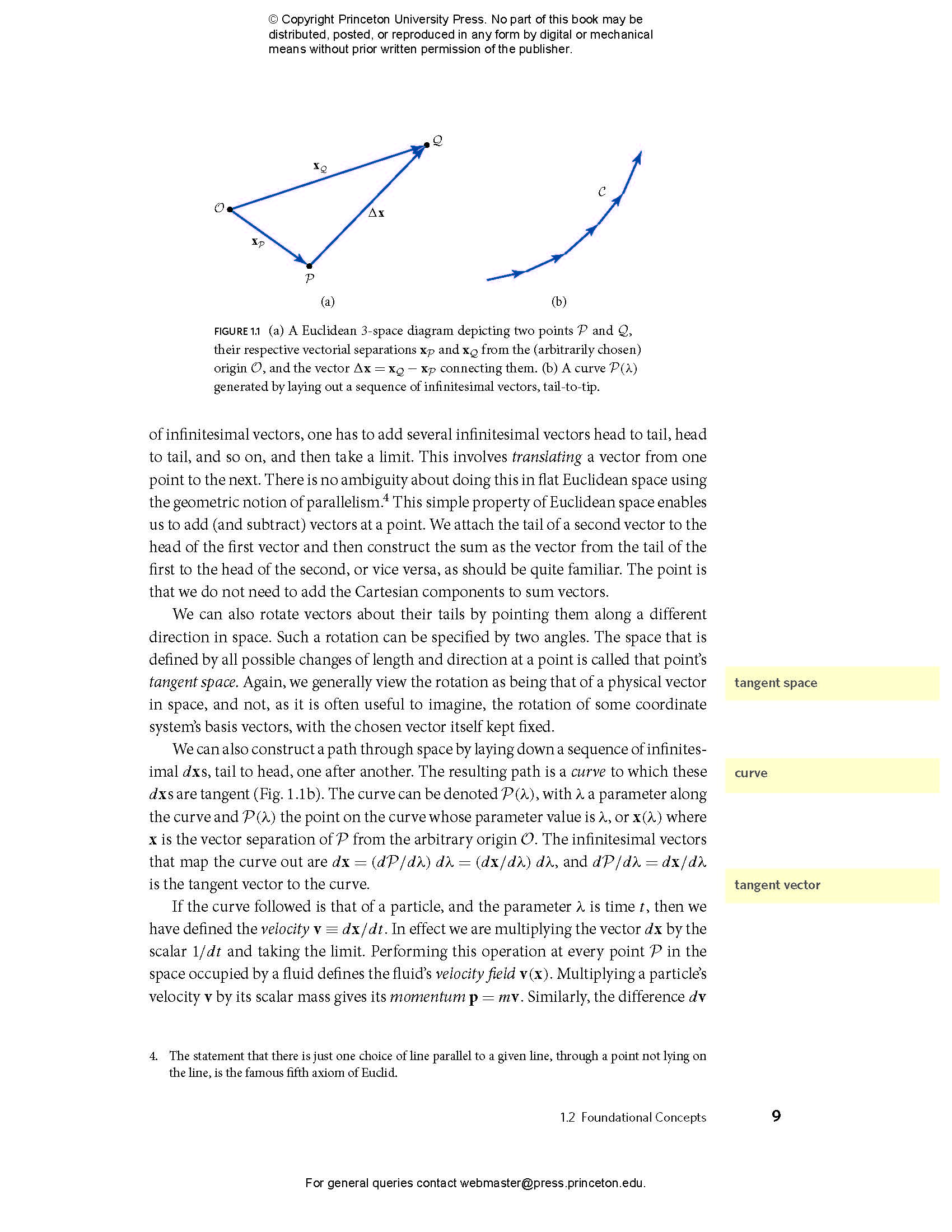
- 1.2 Foundational Concepts
- 1.3 Tensor Algebra without a Coordinate System
- 1.4 Particle Kinetics and Lorentz Force in Geometric Language
- 1.5 Component Represe van der Waalsntation of Tensor Algebra
- 1.5.1 Slot-Naming Index Notation
- 1.5.2 Particle Kinetics in Index Notation
- 1.6 Orthogonal Transformations of Bases
- 1.7 Differentiation of Scalars, Vectors, and Tensors; Cross Product and Curl
- 1.8 Volumes, Integration, and Integral Conservation Laws
- 1.8.1 Gauss’s and Stokes’ Theorems
- 1.9 The Stress Tensor and Momentum Conservation
- 1.9.1 Examples: Electromagnetic Field and Perfect Fluid
- 1.9.2 Conservation of Momentum
- 1.10 Geometrized Units and Relativistic Particles for Newtonian Readers
- 1.10.1 Geometrized Units
- 1.10.2 Energy and Momentum of a Moving Particle
- Bibliographic Note
- 1.1 Introduction
- 2 Special Relativity: Geometric Viewpoint
- 2.1 Overview
- 2.2 Foundational Concepts
- 2.2.1 Inertial Frames, Inertial Coordinates, Events, Vectors, and Spacetime Diagrams
- 2.2.2 The Principle of Relativity and Constancy of Light Speed
- 2.2.3 The Interval and Its Invariance
- 2.3 Tensor Algebra without a Coordinate System
- 2.4 Particle Kinetics and Lorentz Force without a Reference Frame
- 2.4.1 Relativistic Particle Kinetics:World Lines, 4-Velocity, 4-Momentum and Its Conservation, 4-Force
- 2.4.2 Geometric Derivation of the Lorentz Force Law
- 2.5 Component Representation of Tensor Algebra
- 2.5.1 Lorentz Coordinates
- 2.5.2 Index Gymnastics
- 2.5.3 Slot-Naming Notation
- 2.6 Particle Kinetics in Index Notation and in a Lorentz Frame
- 2.7 Lorentz Transformations
- 2.8 Spacetime Diagrams for Boosts
- 2.9 Time Travel
- 2.9.1 Measurement of Time; Twins Paradox
- 2.9.2 Wormholes
- 2.9.3 Wormhole as Time Machine
- 2.10 Directional Derivatives, Gradients, and the Levi-Civita Tensor
- 2.11 Nature of Electric and Magnetic Fields; Maxwell’s Equations
- 2.12 Volumes, Integration, and Conservation Laws
- 2.12.1 Spacetime Volumes and Integration
- 2.12.2 Conservation of Charge in Spacetime
- 2.12.3 Conservation of Particles, Baryon Number, and Rest Mass
- 2.13 Stress-Energy Tensor and Conservation of 4-Momentum
- 2.13.1 Stress-Energy Tensor
- 2.13.2 4-Momentum Conservation
- 2.13.3 Stress-Energy Tensors for Perfect Fluids and Electromagnetic Fields
- Bibliographic Note
- PART II STATISTICAL PHYSICS
- 3 Kinetic Theory
- 3.1 Overview
- 3.2 Phase Space and Distribution Function
- 3.2.1 Newtonian Number Density in Phase Space, 𝒩
- 3.2.2 Relativistic Number Density in Phase Space, 𝒩
- 3.2.3 Distribution Function 𝑓 (x, v, t) for Particles in a Plasma
- 3.2.4 Distribution Function I𝜈/𝜈3 for Photons
- 3.2.5 Mean Occupation Number 𝜂
- 3.3 Thermal-Equilibrium Distribution Functions
- 3.4 Macroscopic Properties of Matter as Integrals over Momentum Space
- 3.4.1 Particle Density 𝑛, Flux S, and Stress Tensor ⊺
- 3.4.2 Relativistic Number-Flux 4-Vector S→ and Stress-Energy Tensor ⊺
- 3.5 Isotropic Distribution Functions and Equations of State
- 3.5.1 Newtonian Density, Pressure, Energy Density, and Equation of State
- 3.5.2 Equations of State for a Nonrelativistic Hydrogen Gas
- 3.5.3 Relativistic Density, Pressure, Energy Density, and Equation of State
- 3.5.4 Equation of State for a Relativistic Degenerate Hydrogen Gas
- 3.5.5 Equation of State for Radiation
- 3.6 Evolution of the Distribution Function: Liouville’s Theorem, the Collisionless Boltzmann Equation, and the Boltzmann Transport Equation
- 3.7 Transport Coefficients
- 3.7.1 Diffusive Heat Conduction inside a Star
- 3.7.2 Order-of-Magnitude Analysis
- 3.7.3 Analysis Using the Boltzmann Transport Equation
- Bibliographic Note
- 4 Statistical Mechanics
- 4.1 Overview
- 4.2 Systems, Ensembles, and Distribution Functions
- 4.2.1 Systems
- 4.2.2 Ensembles
- 4.2.3 Distribution Function
- 4.3 Liouville’s Theorem and the Evolution of the Distribution Function
- 4.4 Statistical Equilibrium
- 4.4.1 Canonical Ensemble and Distribution
- 4.4.2 General Equilibrium Ensemble and Distribution; Gibbs Ensemble; Grand Canonical Ensemble
- 4.4.3 Fermi-Dirac and Bose-Einstein Distributions
- 4.4.4 Equipartition Theorem for Quadratic, Classical Degrees of Freedom
- 4.5 The Microcanonical Ensemble
- 4.6 The Ergodic Hypothesis
- 4.7 Entropy and Evolution toward Statistical Equilibrium
- 4.7.1 Entropy and the Second Law of Thermodynamics
- 4.7.2 What Causes the Entropy to Increase?
- 4.8 Entropy per Particle
- 4.9 Bose-Einstein Condensate
- 4.10 Statistical Mechanics in the Presence of Gravity
- 4.10.1 Galaxies
- 4.10.2 Black Holes
- 4.10.3 The Universe
- 4.10.4 Structure Formation in the Expanding Universe: Violent Relaxation and Phase Mixing
- 4.11 Entropy and Information
- 4.11.1 Information Gained When Measuring the State of a System in a Microcanonical Ensemble
- 4.11.2 Information in Communication Theory
- 4.11.3 Examples of Information Content
- 4.11.4 Some Properties of Information
- 4.11.5 Capacity of Communication Channels; Erasing Information from Computer Memories
- Bibliographic Note
- 5 Statistical Thermodynamics
- 5.1 Overview
- 5.2 Microcanonical Ensemble and the Energy Representation of Thermodynamics
- 5.2.1 Extensive and Intensive Variables; Fundamental Potential
- 5.2.2 Energy as a Fundamental Potential
- 5.2.3 Intensive Variables Identified Using Measuring Devices; First Law of Thermodynamics
- 5.2.4 Euler’s Equation and Form of the Fundamental Potential
- 5.2.5 Everything Deducible from First Law; Maxwell Relations
- 5.2.6 Representations of Thermodynamics
- 5.3 Grand Canonical Ensemble and the Grand-Potential Representation of Thermodynamics
- 5.3.1 The Grand-Potential Representation, and Computation of Thermodynamic Properties as a Grand Canonical Sum
- 5.3.2 Nonrelativistic van der Waals Gas
- 5.4 Canonical Ensemble and the Physical-Free-Energy Representation of Thermodynamics
- 5.4.1 Experimental Meaning of Physical Free Energy
- 5.4.2 Ideal Gas with Internal Degrees of Freedom
- 5.5 Gibbs Ensemble and Representation of Thermodynamics; Phase Transitions and Chemical Reactions
- 5.5.1 Out-of-Equilibrium Ensembles and Their Fundamental Thermodynamic Potentials and Minimum Principles
- 5.5.2 Phase Transitions
- 5.5.3 Chemical Reactions
- 5.6 Fluctuations away from Statistical Equilibrium
- 5.7 Van der Waals Gas: Volume Fluctuations and Gas-to-Liquid Phase Transition
- 5.8 Magnetic Materials
- 5.8.1 Paramagnetism; The Curie Law
- 5.8.2 Ferromagnetism: The Ising Model
- 5.8.3 Renormalization Group Methods for the Ising Model
- 5.8.4 Monte Carlo Methods for the Ising Model
- Bibliographic Note
- 6 Random Processes
- 6.1 Overview
- 6.2 Fundamental Concepts
- 6.2.1 Random Variables and Random Processes
- 6.2.2 Probability Distributions
- 6.2.3 Ergodic Hypothesis
- 6.3 Markov Processes and Gaussian Processes
- 6.3.1 Markov Processes; RandomWalk
- 6.3.2 Gaussian Processes and the Central Limit Theorem; RandomWalk
- 6.3.3 Doob’s Theorem for Gaussian-Markov Processes, and Brownian Motion
- 6.4 Correlation Functions and Spectral Densities
- 6.4.1 Correlation Functions; Proof of Doob’s Theorem
- 6.4.2 Spectral Densities
- 6.4.3 Physical Meaning of Spectral Density, Light Spectra, and Noise in a Gravitational Wave Detector
- 6.4.4 TheWiener-Khintchine Theorem; Cosmological Density Fluctuations
- 6.5 2-Dimensional Random Processes
- 6.5.1 Cross Correlation and Correlation Matrix
- 6.5.2 Spectral Densities and theWiener-Khintchine Theorem
- 6.6 Noise and Its Types of Spectra
- 6.6.1 Shot Noise, Flicker Noise, and Random-Walk Noise; Cesium Atomic Clock
- 6.6.2 Information Missing from Spectral Density
- 6.7 Filtering Random Processes
- 6.7.1 Filters, Their Kernels, and the Filtered Spectral Density
- 6.7.2 Brownian Motion and RandomWalks
- 6.7.3 Extracting aWeak Signal from Noise: Band-Pass Filter, Wiener’s Optimal Filter, Signal-to-Noise Ratio, and Allan Variance of Clock Noise
- 6.7.4 Shot Noise
- 6.8 Fluctuation-Dissipation Theorem
- 6.8.1 Elementary Version of the Fluctuation-Dissipation Theorem; Langevin Equation, Johnson Noise in a Resistor, and Relaxation Time for Brownian Motion
- 6.8.2 Generalized Fluctuation-Dissipation Theorem; Thermal Noise in a Laser Beam’s Measurement of Mirror Motions; Standard Quantum Limit for Measurement Accuracy and How to Evade It
- 6.9 Fokker-Planck Equation
- 6.9.1 Fokker-Planck for a 1-Dimensional Markov Process
- 6.9.2 Optical Molasses: Doppler Cooling of Atoms
- 6.9.3 Fokker-Planck for a Multidimensional Markov Process; Thermal Noise in an Oscillator
- Bibliographic Note
- PART III OPTICS
- 7 Geometric Optics
- 7.1 Overview
- 7.2 Waves in a Homogeneous Medium
- 7.2.1 Monochromatic Plane Waves; Dispersion Relation
- 7.2.2 Wave Packets
- 7.3 Waves in an Inhomogeneous, Time-Varying Medium: The Eikonal Approximation and Geometric Optics
- 7.3.1 Geometric Optics for a Prototypical Wave Equation
- 7.3.2 Connection of Geometric Optics to Quantum Theory
- 7.3.3 Geometric Optics for a General Wave
- 7.3.4 Examples of Geometric-Optics Wave Propagation
- 7.3.5 Relation to Wave Packets; Limitations of the Eikonal Approximation and Geometric Optics
- 7.3.6 Fermat’s Principle
- 7.4 Paraxial Optics
- 7.4.1 Axisymmetric, Paraxial Systems: Lenses, Mirrors, Telescopes, Microscopes, and Optical Cavities
- 7.4.2 Converging Magnetic Lens for Charged Particle Beam
- 7.5 Catastrophe Optics
- 7.5.1 Image Formation
- 7.5.2 Aberrations of Optical Instruments
- 7.6 Gravitational Lenses
- 7.6.1 Gravitational Deflection of Light
- 7.6.2 Optical Configuration
- 7.6.3 Microlensing
- 7.6.4 Lensing by Galaxies
- 7.7 Polarization
- 7.7.1 Polarization Vector and Its Geometric-Optics Propagation Law
- 7.7.2 Geometric Phase
- Bibliographic Note
- 8 Diffraction
- 8.1 Overview
- 8.2 Helmholtz-Kirchhoff Integral
- 8.2.1 Diffraction by an Aperture
- 8.2.2 Spreading of theWavefront: Fresnel and Fraunhofer Regions
- 8.3 Fraunhofer Diffraction
- 8.3.1 Diffraction Grating
- 8.3.2 Airy Pattern of a Circular Aperture: Hubble Space Telescope
- 8.3.3 Babinet’s Principle
- 8.4 Fresnel Diffraction
- 8.4.1 Rectangular Aperture, Fresnel Integrals, and the Cornu Spiral
- 8.4.2 Unobscured Plane Wave
- 8.4.3 Fresnel Diffraction by a Straight Edge: Lunar Occultation of a Radio Source
- 8.4.4 Circular Apertures: Fresnel Zones and Zone Plates
- 8.5 Paraxial Fourier Optics
- 8.5.1 Coherent Illumination
- 8.5.2 Point-Spread Functions
- 8.5.3 Abbé’s Description of Image Formation by a Thin Lens
- 8.5.4 Image Processing by a Spatial Filter in the Focal Plane of a Lens: High-Pass, Low-Pass, and Notch Filters; Phase-Contrast Microscopy
- 8.5.5 Gaussian Beams: Optical Cavities and Interferometric Gravitational-Wave Detectors
- 8.6 Diffraction at a Caustic
- Bibliographic Note
- 9 Interference and Coherence
- 9.1 Overview
- 9.2 Coherence
- 9.2.1 Young’s Slits
- 9.2.2 Interference with an Extended Source: Van Cittert-Zernike Theorem
- 9.2.3 More General Formulation of Spatial Coherence; Lateral Coherence Length
- 9.2.4 Generalization to 2 Dimensions
- 9.2.5 Michelson Stellar Interferometer; Astronomical Seeing
- 9.2.6 Temporal Coherence
- 9.2.7 Michelson Interferometer and Fourier-Transform Spectroscopy
- 9.2.8 Degree of Coherence; Relation to Theory of Random Processes
- 9.3 Radio Telescopes
- 9.3.1 Two-Element Radio Interferometer
- 9.3.2 Multiple-Element Radio Interferometers
- 9.3.3 Closure Phase
- 9.3.4 Angular Resolution
- 9.4 Etalons and Fabry-Perot Interferometers
- 9.4.1 Multiple-Beam Interferometry; Etalons
- 9.4.2 Fabry-Perot Interferometer and Modes of a Fabry-Perot Cavity with Spherical Mirrors
- 9.4.3 Fabry-Perot Applications: Spectrometer, Laser, Mode-Cleaning Cavity, Beam-Shaping Cavity, PDH Laser Stabilization, Optical Frequency Comb
- 9.5 Laser Interferometer Gravitational-Wave Detectors
- 9.6 Power Correlations and Photon Statistics: Hanbury Brown and Twiss Intensity Interferometer
- Bibliographic Note
- 10 Nonlinear Optics
- 10.1 Overview
- 10.2 Lasers
- 10.2.1 Basic Principles of the Laser
- 10.2.2 Types of Lasers and Their Performances and Applications
- 10.2.3 Ti:Sapphire Mode-Locked Laser
- 10.2.4 Free Electron Laser
- 10.3 Holography
- 10.3.1 Recording a Hologram
- 10.3.2 Reconstructing the 3-Dimensional Image from a Hologram
- 10.3.3 Other Types of Holography; Applications
- 10.4 Phase-Conjugate Optics
- 10.5 Maxwell’s Equations in a Nonlinear Medium; Nonlinear Dielectric Susceptibilities; Electro-Optic Effects
- 10.6 Three-Wave Mixing in Nonlinear Crystals
- 10.6.1 Resonance Conditions for Three-Wave Mixing
- 10.6.2 Three-Wave-Mixing Evolution Equations in a Medium That Is Dispersion-Free and Isotropic at Linear Order
- 10.6.3 Three-Wave Mixing in a Birefringent Crystal: Phase Matching and Evolution Equations
- 10.7 Applications of Three-Wave Mixing: Frequency Doubling, Optical Parametric Amplification, and Squeezed Light
- 10.7.1 Frequency Doubling
- 10.7.2 Optical Parametric Amplification
- 10.7.3 Degenerate Optical Parametric Amplification: Squeezed Light
- 10.8 Four-Wave Mixing in Isotropic Media
- 10.8.1 Third-Order Susceptibilities and Field Strengths
- 10.8.2 Phase Conjugation via Four-Wave Mixing in CS2 Fluid
- 10.8.3 Optical Kerr Effect and Four-Wave Mixing in an Optical Fiber
- Bibliographic Note
- PART IV ELASTICITY
- 11 Elastostatics
- 11.1 Overview
- 11.2 Displacement and Strain
- 11.2.1 Displacement Vector and Its Gradient
- 11.2.2 Expansion, Rotation, Shear, and Strain
- 11.3 Stress, Elastic Moduli, and Elastostatic Equilibrium
- 11.3.1 Stress Tensor
- 11.3.2 Realm of Validity for Hooke’s Law
- 11.3.3 Elastic Moduli and Elastostatic Stress Tensor
- 11.3.4 Energy of Deformation
- 11.3.5 Thermoelasticity
- 11.3.6 Molecular Origin of Elastic Stress; Estimate of Moduli
- 11.3.7 Elastostatic Equilibrium: Navier-Cauchy Equation
- 11.4 Young’s Modulus and Poisson’s Ratio for an Isotropic Material: A Simple Elastostatics Problem
- 11.5 Reducing the Elastostatic Equations to 1 Dimension for a Bent Beam: Cantilever Bridge, Foucault Pendulum, DNA Molecule, Elastica
- 11.6 Buckling and Bifurcation of Equilibria
- 11.6.1 Elementary Theory of Buckling and Bifurcation
- 11.6.2 Collapse of theWorld Trade Center Buildings
- 11.6.3 Buckling with Lateral Force; Connection to Catastrophe Theory
- 11.6.4 Other Bifurcations: Venus Fly Trap, Whirling Shaft, Triaxial Stars, and Onset of Turbulence
- 11.7 Reducing the Elastostatic Equations to 2 Dimensions for a Deformed Thin Plate: Stress Polishing a Telescope Mirror
- 11.8 Cylindrical and Spherical Coordinates: Connection Coefficients and Components of the Gradient of the Displacement Vector
- 11.9 Solving the 3-Dimensional Navier-Cauchy Equation in Cylindrical Coordinates
- 11.9.1 Simple Methods: Pipe Fracture and Torsion Pendulum
- 11.9.2 Separation of Variables and Green’s Functions: Thermoelastic Noise in Mirrors
- Bibliographic Note
- 12 Elastodynamics
- 12.1 Overview
- 12.2 Basic Equations of Elastodynamics; Waves in a Homogeneous Medium
- 12.2.1 Equation of Motion for a Strained Elastic Medium
- 12.2.2 Elastodynamic Waves
- 12.2.3 Longitudinal SoundWaves
- 12.2.4 Transverse ShearWaves
- 12.2.5 Energy of Elastodynamic Waves
- 12.3 Waves in Rods, Strings, and Beams
- 12.3.1 Compression Waves in a Rod
- 12.3.2 Torsion Waves in a Rod
- 12.3.3 Waves on Strings
- 12.3.4 Flexural Waves on a Beam
- 12.3.5 Bifurcation of Equilibria and Buckling (Once More)
- 12.4 Body Waves and Surface Waves—Seismology and Ultrasound
- 12.4.1 Body Waves
- 12.4.2 EdgeWaves
- 12.4.3 Green’s Function for a Homogeneous Half-Space
- 12.4.4 Free Oscillations of Solid Bodies
- 12.4.5 Seismic Tomography
- 12.4.6 Ultrasound; Shock Waves in Solids
- 12.5 The Relationship of Classical Waves to Quantum Mechanical Excitations
- Bibliographic Note
- PART V FLUID DYNAMICS
- 13 Foundations of Fluid Dynamics
- 13.1 Overview
- 13.2 The Macroscopic Nature of a Fluid: Density, Pressure, Flow Velocity; Liquids versus Gases
- 13.3 Hydrostatics
- 13.3.1 Archimedes’ Law
- 13.3.2 Nonrotating Stars and Planets
- 13.3.3 Rotating Fluids
- 13.4 Conservation Laws
- 13.5 The Dynamics of an Ideal Fluid
- 13.5.1 Mass Conservation
- 13.5.2 Momentum Conservation
- 13.5.3 Euler Equation
- 13.5.4 Bernoulli’s Theorem
- 13.5.5 Conservation of Energy
- 13.6 Incompressible Flows
- 13.7 Viscous Flows with Heat Conduction
- 13.7.1 Decomposition of the Velocity Gradient into Expansion, Vorticity, and Shear
- 13.7.2 Navier-Stokes Equation
- 13.7.3 Molecular Origin of Viscosity
- 13.7.4 Energy Conservation and Entropy Production
- 13.7.5 Reynolds Number
- 13.7.6 Pipe Flow
- 13.8 Relativistic Dynamics of a Perfect Fluid
- 13.8.1 Stress-Energy Tensor and Equations of Relativistic Fluid Mechanics
- 13.8.2 Relativistic Bernoulli Equation and Ultrarelativistic Astrophysical Jets
- 13.8.3 Nonrelativistic Limit of the Stress-Energy Tensor
- Bibliographic Note
- 14 Vorticity
- 14.1 Overview
- 14.2 Vorticity, Circulation, and Their Evolution
- 14.2.1 Vorticity Evolution
- 14.2.2 Barotropic, Inviscid, Compressible Flows: Vortex Lines Frozen into Fluid
- 14.2.3 Tornados
- 14.2.4 Circulation and Kelvin’s Theorem
- 14.2.5 Diffusion of Vortex Lines
- 14.2.6 Sources of Vorticity
- 14.3 Low-Reynolds-Number Flow—Stokes Flow and Sedimentation
- 14.3.1 Motivation: Climate Change
- 14.3.2 Stokes Flow
- 14.3.3 Sedimentation Rate
- 14.4 High-Reynolds-Number Flow—Laminar Boundary Layers
- 14.4.1 Blasius Velocity Profile Near a Flat Plate: Stream Function and Similarity Solution
- 14.4.2 Blasius Vorticity Profile
- 14.4.3 Viscous Drag Force on a Flat Plate
- 14.4.4 Boundary Layer Near a Curved Surface: Separation
- 14.5 Nearly Rigidly Rotating Flows—Earth’s Atmosphere and Oceans
- 14.5.1 Equations of Fluid Dynamics in a Rotating Reference Frame
- 14.5.2 Geostrophic Flows
- 14.5.3 Taylor-Proudman Theorem
- 14.5.4 Ekman Boundary Layers
- 14.6 Instabilities of Shear Flows—Billow Clouds and Turbulence in the Stratosphere
- 14.6.1 Discontinuous Flow: Kelvin-Helmholtz Instability
- 14.6.2 Discontinuous Flow with Gravity
- 14.6.3 Smoothly Stratified Flows: Rayleigh and Richardson Criteria for Instability
- Bibliographic Note
- 15 Turbulence
- 15.1 Overview
- 15.2 The Transition to Turbulence—Flow Past a Cylinder
- 15.3 Empirical Description of Turbulence
- 15.3.1 The Role of Vorticity in Turbulence
- 15.4 Semiquantitative Analysis of Turbulence
- 15.4.1 Weak-Turbulence Formalism
- 15.4.2 Turbulent Viscosity
- 15.4.3 TurbulentWakes and Jets; Entrainment; the Coanda Effect
- 15.4.4 Kolmogorov Spectrum for Fully Developed, Homogeneous, Isotropic Turbulence
- 15.5 Turbulent Boundary Layers
- 15.5.1 Profile of a Turbulent Boundary Layer
- 15.5.2 Coanda Effect and Separation in a Turbulent Boundary Layer
- 15.5.3 Instability of a Laminar Boundary Layer
- 15.5.4 Flight of a Ball
- 15.6 The Route to Turbulence—Onset of Chaos
- 15.6.1 Rotating Couette Flow
- 15.6.2 Feigenbaum Sequence, Poincaré Maps, and the Period-Doubling Route to Turbulence in Convection
- 15.6.3 Other Routes to Turbulent Convection
- 15.6.4 Extreme Sensitivity to Initial Conditions
- Bibliographic Not
- 16 Waves
- 16.1 Overview
- 16.2 Gravity Waves on and beneath the Surface of a Fluid
- 16.2.1 Deep-Water Waves and Their Excitation and Damping
- 16.2.2 Shallow-Water Waves
- 16.2.3 Capillary Waves and Surface Tension
- 16.2.4 Helioseismology
- 16.3 Nonlinear Shallow-Water Waves and Solitons
- 16.3.1 Korteweg–de Vries (KdV) Equation
- 16.3.2 Physical Effects in the KdV Equation
- 16.3.3 Single-Soliton Solution
- 16.3.4 Two-Soliton Solution
- 16.3.5 Solitons in Contemporary Physics
- 16.4 Rossby Waves in a Rotating Fluid
- 16.5 Sound Waves
- 16.5.1 Wave Energy
- 16.5.2 Sound Generation
- 16.5.3 Radiation Reaction, Runaway Solutions, and Matched Asymptotic Expansions
- Bibliographic Note
- 17 Compressible and Supersonic Flow
- 17.1 Overview
- 17.2 Equations of Compressible Flow
- 17.3 Stationary, Irrotational, Quasi-1-Dimensional Flow
- 17.3.1 Basic Equations; Transition from Subsonic to Supersonic Flow
- 17.3.2 Setting up a Stationary, Transonic Flow
- 17.3.3 Rocket Engines
- 17.4 1-Dimensional, Time-Dependent Flow
- 17.4.1 Riemann Invariants
- 17.4.2 Shock Tube
- 17.5 Shock Fronts
- 17.5.1 Junction Conditions across a Shock; Rankine-Hugoniot Relations
- 17.5.2 Junction Conditions for Ideal Gas with Constant γ
- 17.5.3 Internal Structure of a Shock
- 17.5.4 Mach Cone
- 17.6 Self-Similar Solutions—Sedov-Taylor Blast Wave
- 17.6.1 The Sedov-Taylor Solution
- 17.6.2 Atomic Bomb
- 17.6.3 Supernovae
- Bibliographic Note
- 18 Convection
- 18.1 Overview
- 18.2 Diffusive Heat Conduction—Cooling a Nuclear Reactor; Thermal Boundary Layers
- 18.3 Boussinesq Approximation
- 18.4 Rayleigh-Bénard Convection
- 18.5 Convection in Stars
- 18.6 Double Diffusion—Salt Fingers
- Bibliographic Note
- 19 Magnetohydrodynamics
- 19.1 Overview
- 19.2 Basic Equations of MHD
- 19.2.1 Maxwell’s Equations in the MHD Approximation
- 19.2.2 Momentum and Energy Conservation
- 19.2.3 Boundary Conditions
- 19.2.4 Magnetic Field and Vorticity
- 19.3 Magnetostatic Equilibria
- 19.3.1 Controlled Thermonuclear Fusion
- 19.3.2 Z-Pinch
- 19.3.3 ⊝-Pinch
- 19.3.4 Tokamak
- 19.4 Hydromagnetic Flows
- 19.5 Stability of Magnetostatic Equilibria
- 19.5.1 Linear Perturbation Theory
- 19.5.2 Z-Pinch: Sausage and Kink Instabilities
- 19.5.3 The ⊝-Pinch and Its Toroidal Analog; Flute Instability; Motivation for Tokamak
- 19.5.4 Energy Principle and Virial Theorems
- 19.6 Dynamos and Reconnection of Magnetic Field Lines
- 19.6.1 Cowling’s Theorem
- 19.6.2 Kinematic Dynamos
- 19.6.3 Magnetic Reconnection
- 19.7 Magnetosonic Waves and the Scattering of Cosmic Rays
- 19.7.1 Cosmic Rays
- 19.7.2 Magnetosonic Dispersion Relation
- 19.7.3 Scattering of Cosmic Rays by Alfvén Waves
- Bibliographic Note
- PART VI PLASMA PHYSICS
- 20 The Particle Kinetics of Plasma
- 20.1 Overview
- 20.2 Examples of Plasmas and Their Density-Temperature Regimes
- 20.2.1 Ionization Boundary
- 20.2.2 Degeneracy Boundary
- 20.2.3 Relativistic Boundary
- 20.2.4 Pair-Production Boundary
- 20.2.5 Examples of Natural and Human-Made Plasmas
- 20.3 Collective Effects in Plasmas—Debye Shielding and Plasma Oscillations
- 20.3.1 Debye Shielding
- 20.3.2 Collective Behavior
- 20.3.3 Plasma Oscillations and Plasma Frequency
- 20.4 Coulomb Collisions
- 20.4.1 Collision Frequency
- 20.4.2 The Coulomb Logarithm
- 20.4.3 Thermal Equilibration Rates in a Plasma
- 20.4.4 Discussion
- 20.5 Transport Coefficients
- 20.5.1 Coulomb Collisions
- 20.5.2 Anomalous Resistivity and Anomalous Equilibration
- 20.6 Magnetic Field
- 20.6.1 Cyclotron Frequency and Larmor Radius
- 20.6.2 Validity of the Fluid Approximation
- 20.6.3 Conductivity Tensor
- 20.7 Particle Motion and Adiabatic Invariants
- 20.7.1 Homogeneous, Time-Independent Magnetic Field and No Electric Field
- 20.7.2 Homogeneous, Time-Independent Electric and Magnetic Fields
- 20.7.3 Inhomogeneous, Time-Independent Magnetic Field
- 20.7.4 A Slowly Time-Varying Magnetic Field
- 20.7.5 Failure of Adiabatic Invariants; Chaotic Orbits
- Bibliographic Note
- 21 Waves in Cold Plasmas: Two-Fluid Formalism
- 21.1 Overview
- 21.2 Dielectric Tensor, Wave Equation, and General Dispersion Relation
- 21.3 Two-Fluid Formalism
- 21.4 Wave Modes in an Unmagnetized Plasma
- 21.4.1 Dielectric Tensor and Dispersion Relation for a Cold, Unmagnetized Plasma
- 21.4.2 Plasma Electromagnetic Modes
- 21.4.3 Langmuir Waves and Ion-Acoustic Waves in Warm Plasmas
- 21.4.4 Cutoffs and Resonances
- 21.5 Wave Modes in a Cold, Magnetized Plasma
- 21.5.1 Dielectric Tensor and Dispersion Relation
- 21.5.2 Parallel Propagation
- 21.5.3 Perpendicular Propagation
- 21.5.4 Propagation of Radio Waves in the Ionosphere; Magnetoionic Theory
- 21.5.5 CMA Diagram for Wave Modes in a Cold, Magnetized Plasma
- 21.6 Two-Stream Instability
- Bibliographic Note
- 22 Kinetic Theory of Warm Plasmas
- 22.1 Overview
- 22.2 Basic Concepts of Kinetic Theory and Its Relationship to Two-Fluid Theory
- 22.2.1 Distribution Function and Vlasov Equation
- 22.2.2 Relation of Kinetic Theory to Two-Fluid Theory
- 22.2.3 Jeans’ Theorem
- 22.3 Electrostatic Waves in an Unmagnetized Plasma: Landau Damping
- 22.3.1 Formal Dispersion Relation
- 22.3.2 Two-Stream Instability
- 22.3.3 The Landau Contour
- 22.3.4 Dispersion Relation for Weakly Damped or Growing Waves
- 22.3.5 Langmuir Waves and Their Landau Damping
- 22.3.6 Ion-AcousticWaves and Conditions for Their Landau Damping to Be Weak
- 22.4 Stability of Electrostatic Waves in Unmagnetized Plasmas
- 22.4.1 Nyquist’s Method
- 22.4.2 Penrose’s Instability Criterion
- 22.5 Particle Trapping
- 22.6 N-Particle Distribution Function
- 22.6.1 BBGKY Hierarchy
- 22.6.2 Two-Point Correlation Function
- 22.6.3 Coulomb Correction to Plasma Pressure
- Bibliographic Note
- 23 Nonlinear Dynamics of Plasmas
- 23.1 Overview
- 23.2 Quasilinear Theory in Classical Language
- 23.2.1 Classical Derivation of the Theory
- 23.2.2 Summary of Quasilinear Theory
- 23.2.3 Conservation Laws
- 23.2.4 Generalization to 3 Dimensions
- 23.3 Quasilinear Theory in Quantum Mechanical Language
- 23.3.1 Plasmon Occupation Number η
- 23.3.2 Evolution of 𝜂 for Plasmons via Interaction with Electrons
- 23.3.3 Evolution of 𝑓 for Electrons via Interaction with Plasmons
- 23.3.4 Emission of Plasmons by Particles in the Presence of a Magnetic Field
- 23.3.5 Relationship between Classical and Quantum Mechanical Formalisms
- 23.3.6 Evolution of 𝜂 via Three-Wave Mixing
- 23.4 Quasilinear Evolution of Unstable Distribution Functions—A Bump in the Tail
- 23.4.1 Instability of Streaming Cosmic Rays
- 23.5 Parametric Instabilities; Laser Fusion
- 23.6 Solitons and Collisionless Shock Waves
- Bibliographic Note
- PART VII GENERAL RELATIVITY
- 24 From Special to General Relativity
- 24.1 Overview
- 24.2 Special Relativity Once Again
- 24.2.1 Geometric, Frame-Independent Formulation
- 24.2.2 Inertial Frames and Components of Vectors, Tensors, and Physical Laws
- 24.2.3 Light Speed, the Interval, and Spacetime Diagrams
- 24.3 Differential Geometry in General Bases and in Curved Manifolds
- 24.3.1 Nonorthonormal Bases
- 24.3.2 Vectors as Directional Derivatives; Tangent Space; Commutators
- 24.3.3 Differentiation of Vectors and Tensors; Connection Coefficients
- 24.3.4 Integration
- 24.4 The Stress-Energy Tensor Revisited
- 24.5 The Proper Reference Frame of an Accelerated Observer
- 24.5.1 Relation to Inertial Coordinates; Metric in Proper Reference Frame; Transport Law for Rotating Vectors
- 24.5.2 Geodesic Equation for a Freely Falling Particle
- 24.5.3 Uniformly Accelerated Observer
- 24.5.4 Rindler Coordinates for Minkowski Spacetime
- Bibliographic Note
- 25 Fundamental Concepts of General Relativity
- 25.1 History and Overview
- 25.2 Local Lorentz Frames, the Principle of Relativity, and Einstein’s Equivalence Principle
- 25.3 The Spacetime Metric, and Gravity as a Curvature of Spacetime
- 25.4 Free-Fall Motion and Geodesics of Spacetime
- 25.5 Relative Acceleration, Tidal Gravity, and Spacetime Curvature
- 25.5.1 Newtonian Description of Tidal Gravity
- 25.5.2 Relativistic Description of Tidal Gravity
- 25.5.3 Comparison of Newtonian and Relativistic Descriptions
- 25.6 Properties of the Riemann Curvature Tensor
- 25.7 Delicacies in the Equivalence Principle, and Some Nongravitational Laws of Physics in Curved Spacetime
- 25.7.1 Curvature Coupling in the Nongravitational Laws
- 25.8 The Einstein Field Equation
- 25.8.1 Geometrized Units
- 25.9 Weak Gravitational Fields
- 25.9.1 Newtonian Limit of General Relativity
- 25.9.2 Linearized Theory
- 25.9.3 Gravitational Field outside a Stationary, Linearized Source of Gravity
- 25.9.4 Conservation Laws for Mass, Momentum, and Angular Momentum in Linearized Theory
- 25.9.5 Conservation Laws for a Strong-Gravity Source
- Bibliographic Note
- 26 Relativistic Stars and Black Holes
- 26.1 Overview
- 26.2 Schwarzschild’s Spacetime Geometry
- 26.2.1 The Schwarzschild Metric, Its Connection Coefficients, and Its Curvature Tensors
- 26.2.2 The Nature of Schwarzschild’s Coordinate System, and Symmetries of the Schwarzschild Spacetime
- 26.2.3 Schwarzschild Spacetime at Radii r ≫M: The Asymptotically Flat Region
- 26.2.4 Schwarzschild Spacetime at r ∼M
- 26.3 Static Stars
- 26.3.1 Birkhoff’s Theorem
- 26.3.2 Stellar Interior
- 26.3.3 Local Conservation of Energy and Momentum
- 26.3.4 The Einstein Field Equation
- 26.3.5 Stellar Models and Their Properties
- 26.3.6 Embedding Diagrams
- 26.4 Gravitational Implosion of a Star to Form a Black Hole
- 26.4.1 The Implosion Analyzed in Schwarzschild Coordinates
- 26.4.2 Tidal Forces at the Gravitational Radius
- 26.4.3 Stellar Implosion in Eddington-Finkelstein Coordinates
- 26.4.4 Tidal Forces at r = 0—The Central Singularity
- 26.4.5 Schwarzschild Black Hole
- 26.5 Spinning Black Holes: The Kerr Spacetime
- 26.5.1 The Kerr Metric for a Spinning Black Hole
- 26.5.2 Dragging of Inertial Frames
- 26.5.3 The Light-Cone Structure, and the Horizon
- 26.5.4 Evolution of Black Holes—Rotational Energy and Its Extraction
- 26.6 The Many-Fingered Nature of Time
- Bibliographic Note
- 27 GravitationalWaves and Experimental Tests of General Relativity
- 27.1 Overview
- 27.2 Experimental Tests of General Relativity
- 27.2.1 Equivalence Principle, Gravitational Redshift, and Global Positioning System
- 27.2.2 Perihelion Advance of Mercury
- 27.2.3 Gravitational Deflection of Light, Fermat’s Principle, and Gravitational Lenses
- 27.2.4 Shapiro Time Delay
- 27.2.5 Geodetic and Lense-Thirring Precession
- 27.2.6 Gravitational Radiation Reaction
- 27.3 GravitationalWaves Propagating through Flat Spacetime
- 27.3.1 Weak, PlaneWaves in Linearized Theory
- 27.3.2 Measuring a GravitationalWave by Its Tidal Forces
- 27.3.3 Gravitons and Their Spin and Rest Mass
- 27.4 GravitationalWaves Propagating through Curved Spacetime
- 27.4.1 GravitationalWave Equation in Curved Spacetime
- 27.4.2 Geometric-Optics Propagation of GravitationalWaves
- 27.4.3 Energy and Momentum in GravitationalWaves
- 27.5 The Generation of GravitationalWaves
- 27.5.1 Multipole-Moment Expansion
- 27.5.2 Quadrupole-Moment Formalism
- 27.5.3 Quadrupolar Wave Strength, Energy, Angular Momentum, and Radiation Reaction
- 27.5.4 Gravitational Waves from a Binary Star System
- 27.5.5 GravitationalWaves from Binaries Made of Black Holes, Neutron Stars, or Both: Numerical Relativity
- 27.6 The Detection of Gravitational Waves
- 27.6.1 Frequency Bands and Detection Techniques
- 27.6.2 Gravitational-Wave Interferometers: Overview and Elementary Treatment
- 27.6.3 Interferometer Analyzed in TT Gauge
- 27.6.4 Interferometer Analyzed in the Proper Reference Frame of the Beam Splitter
- 27.6.5 Realistic Interferometers
- 27.6.6 Pulsar Timing Arrays
- Bibliographic Note
- 28 Cosmology
- 28.1 Overview
- 28.2 General Relativistic Cosmology
- 28.2.1 Isotropy and Homogeneity
- 28.2.2 Geometry
- 28.2.3 Kinematics
- 28.2.4 Dynamics
- 28.3 The Universe Today
- 28.3.1 Baryons
- 28.3.2 Dark Matter
- 28.3.3 Photons
- 28.3.4 Neutrinos
- 28.3.5 Cosmological Constant
- 28.3.6 Standard Cosmology
- 28.4 Seven Ages of the Universe
- 28.4.1 Particle Age
- 28.4.2 Nuclear Age
- 28.4.3 Photon Age
- 28.4.4 Plasma Age
- 28.4.5 Atomic Age
- 28.4.6 Gravitational Age
- 28.4.7 Cosmological Age
- 28.5 Galaxy Formation
- 28.5.1 Linear Perturbations
- 28.5.2 Individual Constituents
- 28.5.3 Solution of the Perturbation Equations
- 28.5.4 Galaxies
- 28.6 Cosmological Optics
- 28.6.1 Cosmic Microwave Background
- 28.6.2 Weak Gravitational Lensing
- 28.6.3 Sunyaev-Zel’dovich Effect
- 28.7 Three Mysteries
- 28.7.1 Inflation and the Origin of the Universe
- 28.7.2 Dark Matter and the Growth of Structure
- 28.7.3 The Cosmological Constant and the Fate of the Universe
- Bibliographic Note
- References
- Name Index
- Subject Index
"It is a matter for celebration when two illustrious theoreticians such as Kip Thorne and Roger Blandford provide an in-depth description of the fundamentals of classical physics. . . . The sheer amount of material covered and the effort that has gone into condensing it into a single, beautifully produced volume is extraordinarily impressive."—Malcolm Longair, Nature
"A tour through macroscopic physics that features modern treatments of classical topics and insightful treatments of modern ones. . . . Modern Classical Physics is a magnificent achievement."—Edward Witten, Physics Today
"An excellent tool for students and researchers as an introduction to classical subjects usually missing from most modern physics curricula. . . . A valuable reference for physicists about modern approaches of the development and applications of classical physics."—Miguel A. F. Sanjuán, Contemporary Physics
"Remarkable for its scope and authority, this text offers a new vision of the 'theoretical minimum' of classical physics that all physicists should know, a vision that I hope will revitalize the curricula of many physics departments. On my own shelf it will replace half a dozen dog-eared reference texts."—Scott Tremaine, Institute for Advanced Study
"In an era of fragmentation and specialization, Thorne and Blandford have given us an audacious and splendid grand unification of classical physics, using geometry and space-time as synthesizing principles. Complicated fields as diverse as optics, elasticity, and plasma physics fall to their masterful pedagogy."—William H. Press, University of Texas at Austin
"Comprehensive, concise, and coherent, this is a marvelous summary of the essence of classical physics, somewhat reminiscent of the classic texts of Landau and Lifshitz, and an essential part of any physicist's toolkit. Classical physics is not 'old' physics; it contains many of the most interesting challenges to our understanding of nature and it stands (as in this book) in consistent juxtaposition with quantum physics. This book includes many interesting and often difficult problems, and it will particularly benefit students in the astrophysical and related sciences."—David Stevenson, Caltech
"This is an excellent resource for students and researchers seeking introductions to important subjects neglected by most modern physics curricula."—Jeremy Goodman, Princeton University
"This text is a tour de force. I cannot overemphasize how big a contribution to teaching it will be. It is also likely to instantly become a desk reference for a large part of the research physics community."—Steinn Sigurdsson, Pennsylvania State University